Category: miscellaneous

Hamilton, the Quaternions, and Creativity

Complex numbers have the form

\notag a + \mathrm{i}b, \quad \mathrm{i}^2 = -1,

where \mathrm{i} is the imaginary unit. Quaternions contain two more imaginary units, \mathrm{j} and \mathrm{k}:

\notag a + \mathrm{i}b + \mathrm{j}c + \mathrm{k}d, \quad \mathrm{i}^2 = \mathrm{j}^2 = \mathrm{k}^2 = \mathrm{ijk} = -1.

Sir William Rowan Hamilton discovered the quaternions in 1843 as he walked along the Royal Canal in Dublin, and he famously carved the formulas on a stone of Brougham Bridge. He had for some time been trying to extend the “couplets” a + \mathrm{i}b to “triplets” a + \mathrm{i}b + \mathrm{j}c, but he realized that the requirement |z_1z_2| = |z_1||z_2| for the product of two such numbers could not hold. His key insight was to realize that a fourth imaginary unit, \mathrm{k}, was required and that multiplication would be noncommutative: z_1z_2 \ne z_2z_1 in general.

Hamilton.jpg Sir William Rowan Hamilton. Etching after J. Kirkwood. Credit: Wellcome Library, London. Wellcome Images. Source.

We do not know exactly how Hamilton discovered the quaternions, though his writings provide insights. One way in which he could have constructed the quaternions is by starting with the complex numbers and asking for each of their properties “How might this be different?” Four terms rather than two and noncommutative multiplication are the differences. This approach of identifying the key features of a problem and asking, for each one, “How might this be different?”, is a powerful process for creativity and discovery—a process that anyone can apply to any problem.

For more on the discovery of the quaternions and on how to generate ideas see the article Hamilton’s Discovery of the Quaternions and Creativity in Mathematics by Dennis Sherwood and I in the LMS Newsletter.

Ten Year Anniversary of the Blog

6177441448_5072c214f8_o.gif

This blog is ten years old! I made the first post, Trefethen’s Approximation Theory and Approximation Practice on January 1, 2013. 347 posts and over one million views (for the combined website and blog) later, the aims of the blog are unchanged: to cover numerical linear algebra, software, and numerical analysis and applied mathematics more generally.

In the last three years most of my posts have been in the What Is series, which now has 84 articles. I will continue to add to this series, and will be grateful for any suggestions of topics (please put them in the “Leave a Reply” box below).

There is a lot of content on this site. The best way to find specific information is to use the gray search box at the top right of the page. I use it frequently, often finding things I’d forgotten are here.

Image credit: Bernie Goldbach.

The Ten Most-Viewed Posts of 2022

top10.jpg

According to the WordPress statistics, this blog received over 192,000 visitors and 281,000 views in 2022. These are the ten most-viewed posts published during the year.

  1. Seven Sins of Numerical Linear Algebra
  2. What Is an Eigenvalue?
  3. The Big Six Matrix Factorizations
  4. What Is a Schur Decomposition?
  5. What Is a Permutation Matrix?
  6. What Is the Logarithmic Norm?
  7. What Is the Jordan Canonical Form?
  8. What Is the Frank Matrix?
  9. What Is a Circulant matrix?
  10. What Is a Toeplitz Matrix?

Eight of the posts are from the What Is series, which now contains 83 articles; more will follow in 2023.

The Ten Most-Viewed Posts in 2021

top10.jpg
Image credit: Stuart Miles.

According to the WordPress statistics, this website received over 138,000 visitors and 205,000 views in 2021.

Here are the ten blog posts (published at any time) that received the most views during the year.

  1. Better LaTeX Tables with Booktabs (2019)
  2. What Is a Symmetric Positive Definite Matrix? (2020)
  3. What Is a Condition Number? (2020)
  4. Can We Solve Linear Algebra Problems at Extreme Scale and Low Precisions? (2021)
  5. What Is a Householder Matrix? (2020)
  6. What Is the Cayley–Hamilton Theorem? (2020)
  7. What Is an LU Factorization? (2021)
  8. Five Examples of Proofreading (2017)
  9. What is Numerical Stability? (2020)
  10. What Is the Log-Sum-Exp Function? (2021)

Seven of the posts are from the What Is series, which passed fifty posts in April. The series is ongoing and I have several posts in preparation for early 2022.

Top Ten Posts of 2020

top10.jpg

According to the WordPress statistics, this blog received over 64,000 visitors and 106,000 views in 2020.

Here are the ten most-viewed posts published during the year. All are in the What Is series that I started in March 2020, and which will continue in 2021.

  1. What is Numerical Stability?
  2. What Is a Condition Number?
  3. What Is a Symmetric Positive Definite Matrix?
  4. What Is the Sylvester Equation?
  5. What Is Backward Error?
  6. What Is a Matrix Square Root?
  7. What Is a Fréchet Derivative?
  8. What Is the Complex Step Approximation?
  9. What Is a Cholesky Factorization?
  10. What Is the Hilbert Matrix?

Top Five Posts of 2019

According to the WordPress statistics, this blog received over 39,000 visitors and 65,000 views in 2019. These are the five most-viewed posts published during the year.

list5.jpg
Image courtesy of Stuart Miles at FreeDigitalPhotos.net
  1. Who Invented the Matrix Condition Number?
  2. Numerical Algorithms for High-Performance Computational Science: Highlights of the Meeting
  3. Better LaTeX Tables with Booktabs
  4. Advances in Numerical Linear Algebra Conference and James Hardy Wilkinson Centenary
  5. The Argonne Tapes

Reflections on a SIAM Presidency

180325-2158-00_5921.jpg
The Drexel Dragon, on the Drexel University campus a couple of blocks from SIAM.
180325-2151-31_5912.jpg
Face Fragment (1975) sculpture, a block from SIAM.

My two-year term as SIAM President ended on December 31, 2018. It’s been an exciting and enjoyable two years, not least because of the excellent SIAM staff, leadership and other volunteers I’ve worked with.

My blog post Taking Up the SIAM Presidency and my SIAM News article Evolving and Innovating set out some ideas that I wanted to pursue during my two years as president. I will not attempt to review these here, but just list five highlights from the last two years.

  • We held the SIAM ADVANCE in April 2018: a two-day strategic planning workshop attended by 25 officers, staff, and other members of the SIAM community. The many ideas that emerged from the event are summarized in an 80-page report provided to the SIAM Council and Board of Trustees. Many of these have already been acted upon, others are in progress, and yet more will be considered in the future. My SIAM News article Advancing SIAM gives more details of the workshop.
  • A new journal SIAM Journal on Mathematics of Data Science was created. The first issue will be published in the first few months of 2019.
  • A new SIAM book series Data Science was created.
  • A new SIAG, the SIAM Activity Group on Applied and Computational Discrete Algorithms was approved and will begin operation in 2019.
  • The new SIAM website was launched (in June 2018).
180325-2148-44_5906.jpg
The location of the SIAM office: 3600 Market Street, Philadelphia.

Here is a summary of my presidency in numbers:

  • 12 trips to the USA (with 0 upgrades from economy class to business class).
  • 8 visits to SIAM headquarters and 1 SIAM staff meeting attended.
  • 20 “From the SIAM President” columns written for SIAM News: they are listed here.
  • 2 SIAM Council Meetings chaired and 4 SIAM Board meetings attended.
  • 1 ICIAM board meeting attended and 1 ICIAM board meeting and workshop hosted by SIAM in Philadelphia.
  • 2 meetings of the Joint Policy Board for Mathematics in Washington chaired and 2 attended.
  • Over 230 appointments made to committees and of candidates for elections (with the advice of various SIAM committees).

Top Ten Posts of 2018

top10.jpg

According to the WordPress statistics, this blog received over 42,000 visitors and 73,000 views in 2018. These are the ten most-viewed posts published during the year.

  1. How to Program log z
  2. Tricks and Tips in Numerical Computing
  3. Conversations with Gil Strang
  4. What’s New in MATLAB R2018a?
  5. Numerical Linear Algebra Group 2017
  6. Bohemian Matrices in Manchester
  7. Half Precision Arithmetic: fp16 Versus bfloat16
  8. Palomino Blackwing Pencil Tribute to Ada Lovelace
  9. Joan E. Walsh (1932–2017)
  10. Lectures on Multiprecision Algorithms in Kácov

In addition, the article Differentiation With(out) a Difference in my SIAM News “From the SIAM President” column was the most viewed SIAM News article of 2018.

Taking Up the SIAM Presidency

I am honored to be taking over the reins from Pam Cook as president of the Society for Industrial and Applied Mathematics (SIAM) for the next two years, starting January 1, 2017. Pam remains as past-president during 2017. I look forward to helping to address the challenges facing SIAM and to working with the excellent SIAM officers and staff.

160420-0859-44-4096-Edit.jpg
SIAM headquarters, Philadelphia.

Eighteen months ago I wrote a “candidate statement” for the fall 2015 SIAM elections. The comments I made then remain valid and so I thought it would be worth reproducing the statement here.

The January/February 2017 issue of SIAM News will contain my first From the SIAM President column, in which I give further thoughts on SIAM’s future.

I am happy to receive comments from SIAM members or potential members, either in the box below or by email.

Candidate Statement: SIAM is the leading international organization for applied mathematics and has been an important part of my professional life since I joined as a PhD student, 31 years ago. SIAM is the first place that many people turn to for publications, conferences, and news about applied mathematics and it represents the profession nationally and internationally.

I have been fortunate to be involved in the leadership for many years, having spent six years on the Council, eight years on the Board, and having recently served two terms as Vice President At Large (2010-2013).

SIAM faces a number of challenges that, if elected as President, I relish helping to address, working with SIAM members, SIAM officers, and the excellent SIAM staff.

SIAM’s publications remain strong, but are vulnerable to changes in the way scholarly journals operate (open access, article processing charges, etc.). SIAM needs to monitor the situation and respond appropriately, while striving to provide an even greater service to authors, referees and editors, for example by better use of web tools.

SIAM’s membership is also healthy, but SIAM must continue to enhance membership benefits and work hard to attract and retain student members, who are the future of the society, and to provide value for its members in industry.

Book sales are declining globally and in academic publishing it is becoming harder to find authors with the time to write a book. Nevertheless, the SIAM book program is in a strong position and the 2015 review of the program that I chaired has produced a list of recommendations that should help it to thrive.

SIAM conferences are a terrific place to learn about the latest developments in the subject, meet SIAM staff, browse SIAM books, and attend a business meeting. Attendances continue to grow (the SIAM CSE meeting in Salt Lake City last March was the largest ever SIAM meeting, with over 1700 attendees), but in any given year, the majority of SIAM’s 14,000 members do not attend a SIAM conference. Audio and slide captures of selected lectures are made available on SIAM Presents, but we need to do more to help members engage in virtual participation.

The SIAM web site has provided sterling service for a number of years, but is in need of a major redesign, which is underway. This is an excellent opportunity to integrate better the many services (conferences, journals, books, membership, activity groups, chapters, sections, etc.) in a responsive design. Beyond the core website, SIAM has a strong social media presence, posts a wide variety of videos on its YouTube channel, hosts SIAM Blogs (which I was involved in setting up in 2013), has recently made SIAM News available online, and has SIAM Connect and SIAM Unwrapped as further outlets. Optimizing the use of all these communication tools will be an ongoing effort.

These are just some of the challenges facing SIAM in the future as it continues to play a global leadership role for applied mathematics.

July 2015

Mathematical Word Processing: Historical Snippets

Matthew G. Kirschenbaum’s recent book Track Changes: A Literary History of Word Processing contains a lot of interesting detail about the early days of word processing, covering the period 1964 to 1984. Most of the book concerns non-scientific writing, though \TeX gets a brief mention.

Inspired by the book, I thought it might be useful to collect some information on early mathematical wordprocessing. Little information of this kind seems to be available online.

It is first worth noting that before the advent of word processors papers were typed on a typewriter and mathematical symbols were typically filled in by hand, as in this example from A Study of the Matrix Exponential (1975) by Charlie Van Loan: vanl75-eq-p15.jpg

Some institutions had the luxury of IBM Selectric typewriters, which had a “golf ball” that could be changed in order to type special characters. (See this page for informative videos about the Selectric.) Here is an example of output from the Selectric, taken from my MSc thesis: high83m-eq224.jpg This illustrates some characteristic weaknesses of typewriter output: superscripts, subscripts, and operators are of the same size as the main symbols and spacing between characters is fixed (as in the vertical bars making up the norm signs here).

In 1980s at the Department of Mathematics at the University of Manchester the word processor Vuwriter was used. It was produced by a spin-off company Vuman Computer Systems, which took its name from “Victoria University of Manchester”, the university’s full name. Vuwriter ran on the Apricot PC, produced by the British company Apricot computers. At least one of my first papers was typed on Vuwriter by the office staff and I still have the original 1984 technical report Computing the Polar Decomposition—with Applications, which I have scanned and is available here. A typical equation from the report is this one:

high84p-eq2p2.jpg

The article

Peter Dolton, Comparing Scientific Word Processor Packages: 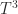T^3 and Vuwriter, The Economic Journal 100, 311-315, 1990

reviews a version of Vuwriter that ran under MS DOS on IBM PC compatibles. Another review is

D. L. Mealand, Word Processing in Greek using Vuwriter Arts: A Test case for Foreign Language Word Processing, Literary and Linguistic Computing 2, 30-33, 1987

which describes a version of the program for use with foreign languages.

The Department of Mathematics at UMIST (which merged with the University of Manchester in 2004) used an MSDOS word processor called ChiWriter.

In the same period I also prepared manuscripts on my own microcomputers: first on a Commodore 64 and then on a Commodore 128 (essentially a Commodore 64 with a screen 80 characters wide rather than 40 characters wide), using a wordprocessor called Vizawrite. For output I used an Epson FX-80 dot matrix printer, and later an Epson LQ 850 (which produced high resolution output thanks to its 24 pin print head, as opposed to the 9 pin print head of the FX-80). Vizawrite was able to take advantage of the Epson printers’ ability to produce subscripts and superscripts, Greek characters, and mathematical symbols. An earlier post links to a scan of my 1985 article Matrix Computations in Basic on a Microcomputer produced in Vizawrite.

In the 1980s some colleagues wrote papers on a Mac. An example (preserved at the Cornell eCommons digital repository) is A Storage Efficient WY Representation for Products of Householder Transformations (1987) by Charlie Van Loan. I think that report was prepared in Mac Write. Here is a sample equation:

vanl87-eq.jpg

Also in the 1980s I built a database of papers that I had read, and wrote a program that could extract the items that I wanted to cite, format them, and print a sorted list. This was a big time-saver for producing reference lists, especially for my PhD thesis. The database was originally held in Superbase for the Commodore C128, with the program written in Superbase’s own language, and was later transferred to PC-File running on an IBM PC-clone with the program converted to GW-Basic. I was essentially building my own much simpler version of BibTeX, which did not exist when I started the database.

I am aware of two good sources of information about technical word processors for the IBM PC. The first is the article

P. K. Wong, Choices for Mathematical Wordprocessing Software, SIAM News 17(6), pp. 8-9, 1984

This article notes that

“There are over 120 wordprocessing programs for the IBM PC alone and the machine is not yet three years old! Of this large number, however, less than half a dozen can claim scientific wordprocessing capabilities, and these have only been available within the past six to nine months.”

The other source is two articles published in the Notices of the American Mathematical Society in the 1980s.

PC Technical Group of IBM PC Users Group of the Boston Computer Society, Technical Wordprocessors for the IBM PC and Compatibles, Notices Amer. Math. Soc. 33, 8-37, 1986

PC Technical Group of IBM PC Users Group of the Boston Computer Society, Technical Wordprocessors for the IBM PC and Compatibles, Part IIB: Reviews, Notices Amer. Math. Soc. 34, 462-491, 1987

These two articles do not appear to be available online. The first of them includes a set of benchmarks, consisting of extracts from technical journals and books, which were used to test the abilities of the packages. The authors make the interesting comment that

“Microsoft chose not to answer our review request for Word, and based on discussion with Word owners, Word is not set up for equations.”

Finally, Roger Horn told me that his book Topics in Matrix Analysis (CUP, 1991), co-authored with Charlie Johnson, was produced from the camera-ready output of the 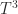T^3 wordprocessing system (reviewed in this 1988 article and in the SIAM News article above). 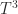T^3 was chosen because \TeX was not available on PCs when work on the the book began. It must have been a huge effort to produce this 607-page book in this way!

If you have any information to add, please put it in the “Leave a Reply” box below.

Acknowledgement: thanks to Christopher Baker and David Silvester for comments on a draft of this post.