Matrix rank is an important concept in linear algebra. While rank deficiency can be a sign of an incompletely or improperly specified problem (a singular system of linear equations, for example), in some problems low rank of a matrix is a desired property or outcome. Here we present some fundamental rank relations in a concise form useful for reference. These are all immediate consequences of the singular value decomposition (SVD), but we give elementary (albeit not entirely self-contained) proofs of them.
The rank of a matrix is the maximum number of linearly independent columns, which is the dimension of the range space of
,
. An important but non-obvious fact is that this is the same as the maximum number of linearly independent rows (see (5) below).
A rank- matrix has the form
, where
and
are nonzero vectors. Every column is a multiple of
and every row is a multiple of
. A sum of
rank-
matrices has the form
Each column of is a linear combination of the vectors
,
, …,
, so
has at most
linearly independent columns, that is,
has rank at most
. In fact,
if
and
have rank
, as follows from (4) below. Any rank-
matrix can be written in the form
with
and
of rank
; indeed this is the full-rank factorization below.
Here are some fundamental rank equalities and inequalities.
Rank-Nullity Theorem
The rank-nullity theorem says that
where is the null space of
.
Rank Bound
The rank cannot exceed the number of columns, or, by (5) below, the number of rows:
Rank of a Sum
For any and
of the same dimension,
The upper bound follows from the fact that the dimension of the sum of two subspaces cannot exceed the sum of the dimensions of the subspaces. Interestingly, the upper bound is also a corollary of the bound (3) for the rank of a matrix product, because
For the lower bound, writing and applying the upper bound gives
, and likewise with the roles of
and
interchanged.
Rank of 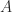 and
and 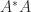
For any ,
Indeed implies
, and
implies
, which implies
. Hence the null spaces of
and
are the same. The equality (2) follows from the rank-nullity theorem.
Rank of a General Product
For any and
for which the product
is defined,
If then
, so the columns of
are linear combinations of those of
and so
cannot have more linearly independent columns than
, that is,
. Using (5) below, we then have
The latter inequality can be proved without using (5) (our proof of which uses (3)), as follows. Suppose . Let the columns of
span
, so that
has
columns and
for some matrix
with
columns. Now
by the first part, so
for some nonzero
. But then
, which contradicts the linear independence of the columns of
, so we must have
.
Rank of a Product of Full-Rank Matrices
We have
We note that and
are both nonsingular
matrices by (2), so their product has rank
. Using (3),
and hence .
Another important relation is
This is a consequence of the equality for nonsingular
and
.
Ranks of 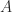 and
and 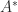
By (2) and (3) we have . Interchanging the roles of
and
gives
and so
In other words, the rank of is equal to the maximum number of linearly independent rows as well as the maximum number of linearly independent columns.
Full-Rank Factorization
has rank
if and only if
for some
and
, both of rank
, and this is called a full-rank factorization. The existence of such a factorization implies that
by (4). Conversely, suppose that
has rank
. Let the columns of
form a basis for the range space of
. Then there are
-vectors
such that
,
, and with
we have
. Finally,
by (3), and since
we have
.
Rank and Minors
A characterization of rank that is sometimes used as the definition is that it is the size of the largest nonsingular square submatrix. Equivalently, the rank is the size of the largest nonzero minor, where a minor of size is the determinant of a
submatrix.
rank(AB) and rank(BA)
Although and
have some properties in common when both products are defined (notably they have the same nonzero eigenvalues),
is not always equal to
. A simple example is
and
with
and
orthogonal vectors:
but
. An example with square
and
is
Note that and
, where
has
in the
th position and zeros everywhere else. Such matrices are easy to manipulate in this form (e.g.,
) and are useful for constructing examples.
How to Find Rank
If we have a full-rank factorization of then we can read off the rank from the dimensions of the factors. But finding a full-rank factorization is a nontrivial task. The ultimate full-rank factorization is the SVD
where and
are orthogonal,
, where
, and
. The rank of
is
, the number of nonzero singular values.
In floating-point arithmetic, the standard algorithms for computing the SVD are numerically stable, that is, the computed singular values are the exact singular values of a matrix with
, where
is a constant and
is the unit roundoff. Unfortunately,
will typically be full rank when
is rank deficient. For example, consider this computation.
>> n = 4; A = zeros(n); A(:) = 1:n^2, svd(A)
A =
1 5 9 13
2 6 10 14
3 7 11 15
4 8 12 16
ans =
3.8623e+01
2.0713e+00
1.5326e-15
1.3459e-16
The matrix has rank and the two zero singular values are approximated by computed singular values of order
. In general, we have no way to know whether tiny computed singular values signify exactly zero singular values. In practice, one typically defines a numerical rank based on a threshold and regards computed singular values less than the threshold as zero. Indeed the MATLAB
rank function computes the rank as the number of singular values exceeding , where
is the largest computed singular value. If the data from which the matrix is constructed is uncertain then the definition of numerical rank should take into account the level of uncertainty in the data. Dealing with rank deficiency in the presence of data errors and in finite precision arithmetic is a tricky business.
References
An excellent reference for further rank relations is Horn and Johnson. Stewart describes some of the issues associated with rank-deficient matrices in practical computation.
- Roger A. Horn and Charles R. Johnson, Matrix Analysis, second edition, Cambridge University Press, 2013. My review of the second edition.
- G. W. Stewart, Rank Degeneracy, SIAM J. Sci. Statist. Comput. 5 (2), 403–413, 1984

