The spectral radius of a square matrix
is the largest absolute value of any eigenvalue of
:
For Hermitian matrices (or more generally normal matrices, those satisfying ) the spectral radius is just the
-norm,
. What follows is most interesting for nonnormal matrices.
Two classes of matrices for which the spectral radius is known are as follows.
- Unitary matrices (
): these have all their eigenvalues on the unit circle and so
.
- Nilpotent matrices (
for some positive integer
): such matrices have only zero eigenvalues, so
, even though
can be arbitrarily large.
The spectral radius of is not necessarily an eigenvalue, though it is if
is nonnegative (see below).
Bounds
The spectral radius is bounded above by any consistent matrix norm (one satisfying for all
and
), for example any matrix
-norm.
Theorem 1. For any
and any consistent matrix norm,
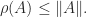
However, the spectral radius is not a norm and it can be zero when the -norms are of order
, as illustrated by the nilpotent matrix
Limit of Norms of Powers
The spectral radius can be expressed as a limit of norms of matrix powers.
Theorem 2 (Gelfand). For
and any matrix norm,
.
The theorem implies that for large enough ,
is a good approximation to
. The use of this formula with repeated squaring of
has been analyzed by Friedland (1991) and Wilkinson (1965). However, squaring requires
flops for a full matrix, so this approach is expensive.
Spectral Radius of a Product
Little can be said about the spectral radius of a product of two matrices. The example
shows that we can have when
. On the other hand, for
we have .
Condition Number Lower Bound
For a nonsingular matrix , by applying Theorem 1 to
and
we obtain
This bound can be very weak for nonnormal matrices.
Power Boundedness
In many situations we wish to know whether the powers of a matrix converge to zero. The spectral radius gives a necessary and sufficient condition for convergence.
Theorem 3. For
,
as
if and only if
.
The proof of Theorem 3 is straightforward if is diagonalizable and it can be done in general using the Jordan canonical form.
Computing the Spectral Radius
Suppose has a dominant eigenvalue
, that is,
,
. Then
. The dominant eigenvalue
can be computed by the power method.
In this pseudocode, norm(x) denotes the -norm of
x.
Choose n-vector q_0 such that norm(q_0) = 1.
for k=1,2,...
z_k = A q_{k-1} % Apply A.
q_k = z_k / norm(z_k) % Normalize.
mu_k = q_k^*Aq_k % Rayleigh quotient.
end
The normalization is to avoid overflow and underflow and the are approximations to
.
If has a nontrivial component in the direction of the eigenvector corresponding to the dominant eigenvalue then the power method converges linearly, with a constant that depends on the ratio of the spectral radius to the magnitude of the next largest eigenvalue in magnitude.
Here is an example where the power method converges quickly, thanks to the substantial ratio of between the spectral radius and next largest eigenvalue in magnitude.
>> rng(1); A = rand(4); eig_abs = abs(eig(A)), q = rand(4,1);
>> for k = 1:5, q = A*q; q = q/norm(q); mu = q'*A*q;
>> fprintf('%1.0f %7.4e\n',k,mu)
>> end
eig_abs =
1.3567e+00
2.0898e-01
2.5642e-01
1.9492e-01
1 1.4068e+00
2 1.3559e+00
3 1.3580e+00
4 1.3567e+00
5 1.3567e+00
Nonnegative Matrices
For real matrices with nonnegative elements, much more is known about the spectral radius. Perron–Frobenius theory says that if is nonnegative then
is an eigenvalue of
and there is a nonnegative eigenvector
such that
. This is why if you generate a random matrix in MATLAB using the
rand function, which produces random matrices with elements on , there is always an eigenvalue equal to the spectral radius:
>> rng(1); A = rand(4); e = sort(eig(A)) e = -2.0898e-01 1.9492e-01 2.5642e-01 1.3567e+00
If is stochastic, that is, it is nonnegative and has unit row sums, then
. Indeed
is an eigenvector corresponding to the eigenvalue
, so
, but
, by Theorem 1.
References
- Shmuel Friedland, Revisiting Matrix Squaring, Linear Algebra Appl., 154–156, 59-63, 1991.
- J. H. Wilkinson, The Algebraic Eigenvalue Problem, Oxford University Press, 1965, pp.~615–617.
Related Blog Posts
This article is part of the “What Is” series, available from https://nhigham.com/index-of-what-is-articles/ and in PDF form from the GitHub repository https://github.com/higham/what-is.

 Sir William Rowan Hamilton. Etching after J. Kirkwood. Credit: Wellcome Library, London. Wellcome Images.
Sir William Rowan Hamilton. Etching after J. Kirkwood. Credit: Wellcome Library, London. Wellcome Images. 
 James Wilkinson’s 1963 book Rounding Errors in Algebraic Processes has been hugely influential. It came at a time when the effects of rounding errors on numerical computations in finite precision arithmetic had just starting to be understood, largely due to Wilkinson’s pioneering work over the previous two decades. The book gives a uniform treatment of error analysis of computations with polynomials and matrices and it is notable for making use of backward errors and condition numbers and thereby distinguishing problem sensitivity from the stability properties of any particular algorithm.
James Wilkinson’s 1963 book Rounding Errors in Algebraic Processes has been hugely influential. It came at a time when the effects of rounding errors on numerical computations in finite precision arithmetic had just starting to be understood, largely due to Wilkinson’s pioneering work over the previous two decades. The book gives a uniform treatment of error analysis of computations with polynomials and matrices and it is notable for making use of backward errors and condition numbers and thereby distinguishing problem sensitivity from the stability properties of any particular algorithm.