What Is the Spectral Radius of a Matrix?

The spectral radius \rho(A) of a square matrix A\in\mathbb{C}^{n\times n} is the largest absolute value of any eigenvalue of A:

\notag \rho(A) = \max\{\, |\lambda|: \lambda~ \mbox{is an eigenvalue of}~ A\,\}.

For Hermitian matrices (or more generally normal matrices, those satisfying AA^* = A^*A) the spectral radius is just the 2-norm, \rho(A) = \|A\|_2. What follows is most interesting for nonnormal matrices.

Two classes of matrices for which the spectral radius is known are as follows.

  • Unitary matrices (U^*U=I): these have all their eigenvalues on the unit circle and so \rho(U) = 1.
  • Nilpotent matrices (A^p = 0 for some positive integer p): such matrices have only zero eigenvalues, so \rho(A) = 0, even though \|A\| can be arbitrarily large.

The spectral radius of A is not necessarily an eigenvalue, though it is if A is nonnegative (see below).

Bounds

The spectral radius is bounded above by any consistent matrix norm (one satisfying \|AB\| \le \|A\|\|B\| for all A and B), for example any matrix p-norm.

Theorem 1. For any A\in\mathbb{C}^{n\times n} and any consistent matrix norm,

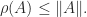
\notag \rho(A) \le \|A\|.

However, the spectral radius is not a norm and it can be zero when the p-norms are of order 1, as illustrated by the nilpotent matrix

\notag A = \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \;\Rightarrow\; \rho(A) = 0, \quad \|A\|_p = 1, \; 1 \le p \le \infty.

Limit of Norms of Powers

The spectral radius can be expressed as a limit of norms of matrix powers.

Theorem 2 (Gelfand). For A\in\mathbb{C}^{n\times n} and any matrix norm, \rho(A) = \lim_{k\to\infty}\|A^k\|^{1/k}.

The theorem implies that for large enough k, \|A^k\|^{1/k} is a good approximation to \rho(A). The use of this formula with repeated squaring of A has been analyzed by Friedland (1991) and Wilkinson (1965). However, squaring requires O(n^3) flops for a full matrix, so this approach is expensive.

Spectral Radius of a Product

Little can be said about the spectral radius of a product of two matrices. The example

\notag A = \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}, \quad B = \begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix}, \quad AB = 0

shows that we can have \rho(AB) = 0 when \rho(A) = \rho(B) = 1. On the other hand, for

\notag A = \begin{bmatrix} 0 & 1 \\ 0 & 1 \end{bmatrix}, \quad B = \begin{bmatrix} 0 & 0 \\ 1 & 1 \end{bmatrix}, \quad AB = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}

we have 1 = \rho(A)\rho(B) < \rho(AB) = 2.

Condition Number Lower Bound

For a nonsingular matrix A, by applying Theorem 1 to A and A^{-1} we obtain

\notag \begin{aligned}\notag \kappa(A) &= \|A\| \|A^{-1}\| \ge \rho(A) \rho(A^{-1})\\ &= \frac{ \max_i |\lambda_i| } { \min_i |\lambda_i| }. \end{aligned}

This bound can be very weak for nonnormal matrices.

Power Boundedness

In many situations we wish to know whether the powers of a matrix converge to zero. The spectral radius gives a necessary and sufficient condition for convergence.

Theorem 3. For A\in\mathbb{C}^{n\times n}, A^k\to0 as k\to\infty if and only if \rho(A) < 1.

The proof of Theorem 3 is straightforward if A is diagonalizable and it can be done in general using the Jordan canonical form.

Computing the Spectral Radius

Suppose A has a dominant eigenvalue \lambda_1, that is, |\lambda_1| > |\lambda_i|, i=2\colon n. Then \rho(A) = |\lambda_1|. The dominant eigenvalue \lambda_1 can be computed by the power method.

In this pseudocode, norm(x) denotes the 2-norm of x. 

Choose n-vector q_0 such that norm(q_0) = 1.
for k=1,2,...                                         
    z_k = A q_{k-1}            % Apply A.
    q_k = z_k / norm(z_k)      % Normalize.     
    mu_k = q_k^*Aq_k           % Rayleigh quotient.
end

The normalization is to avoid overflow and underflow and the |\mu_k| are approximations to \rho(A).

If q_0 has a nontrivial component in the direction of the eigenvector corresponding to the dominant eigenvalue then the power method converges linearly, with a constant that depends on the ratio of the spectral radius to the magnitude of the next largest eigenvalue in magnitude.

Here is an example where the power method converges quickly, thanks to the substantial ratio of 6.49 between the spectral radius and next largest eigenvalue in magnitude. 

>> rng(1); A = rand(4); eig_abs = abs(eig(A)), q = rand(4,1); 
>> for k = 1:5, q = A*q; q = q/norm(q); mu = q'*A*q; 
>>              fprintf('%1.0f %7.4e\n',k,mu)
>> end
eig_abs =
   1.3567e+00
   2.0898e-01
   2.5642e-01
   1.9492e-01
1 1.4068e+00
2 1.3559e+00
3 1.3580e+00
4 1.3567e+00
5 1.3567e+00

Nonnegative Matrices

For real matrices with nonnegative elements, much more is known about the spectral radius. Perron–Frobenius theory says that if A\in\mathbb{R}^{n\times n} is nonnegative then \rho(A) is an eigenvalue of A and there is a nonnegative eigenvector x such that Ax = \rho(A)x. This is why if you generate a random matrix in MATLAB using the rand function, which produces random matrices with elements on (0,1), there is always an eigenvalue equal to the spectral radius: 

>> rng(1);  A = rand(4); e = sort(eig(A))
e =
  -2.0898e-01
   1.9492e-01
   2.5642e-01
   1.3567e+00

If A is stochastic, that is, it is nonnegative and has unit row sums, then \rho(A) = 1. Indeed e = [1,1,\dots,1]^T is an eigenvector corresponding to the eigenvalue 1, so \rho(A) \ge 1, but \rho(A) \le \|A\|_{\infty} = 1, by Theorem 1.

References

  • Shmuel Friedland, Revisiting Matrix Squaring, Linear Algebra Appl., 154–156, 59-63, 1991.
  • J. H. Wilkinson, The Algebraic Eigenvalue Problem, Oxford University Press, 1965, pp.~615–617.

Related Blog Posts

This article is part of the “What Is” series, available from https://nhigham.com/index-of-what-is-articles/ and in PDF form from the GitHub repository https://github.com/higham/what-is.

One thought on “What Is the Spectral Radius of a Matrix?”

  1. I was just studying this! I’m curious to the weak bounds for nonnormal matrices. Is there still something useful we can say about nonnormal matrices and the spectral radius?

    Reply

Leave a comment