Newton methods for minimizing a function  generate a sequence of points
generate a sequence of points  , where the step from
, where the step from  to
to  is along a search direction
is along a search direction  determined from a linear system
determined from a linear system 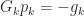 , where
, where  is the gradient and
is the gradient and  is an approximation to the Hessian matrix
is an approximation to the Hessian matrix 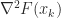 . The equation
. The equation  shows that
shows that  is a descent direction if
is a descent direction if 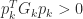 , and in order to guarantee that this condition holds for all
, and in order to guarantee that this condition holds for all  we need
we need  to be positive definite. But even if
to be positive definite. But even if  is the exact Hessian, positive definiteness is not guaranteed far from a minimizer. We can modify the method to ensure definiteness of
is the exact Hessian, positive definiteness is not guaranteed far from a minimizer. We can modify the method to ensure definiteness of  , as with quasi-Newton methods. Or we can perturb the matrix, if necessary, to make it positive definite. Modified Cholesky factorization perturbs and factorizes the matrix at the same time. It is useful in other situations, too, such as in constructing preconditioners and in bounding the distance to a positive semidefinite matrix.
, as with quasi-Newton methods. Or we can perturb the matrix, if necessary, to make it positive definite. Modified Cholesky factorization perturbs and factorizes the matrix at the same time. It is useful in other situations, too, such as in constructing preconditioners and in bounding the distance to a positive semidefinite matrix.
A modified Cholesky factorization of a symmetric matrix 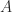 is a factorization
is a factorization 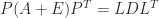 , where
, where 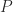 is a permutation matrix,
is a permutation matrix, 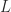 is unit lower triangular, and
is unit lower triangular, and 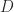 is diagonal or block diagonal and positive definite. It follows that
is diagonal or block diagonal and positive definite. It follows that  is a positive definite matrix.
is a positive definite matrix.
A natural way to compute a modified Cholesky factorization is to modify the Cholesky factorization algorithm. Cholesky factorization fails when it tries to take the square root of a negative quantity or divide by zero. We can avoid both possibilities by increasing nonpositive pivots when they are encountered. This corresponds to making a diagonal perturbation 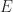 to
to 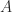 and computing a Cholesky factorization
and computing a Cholesky factorization 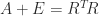 . However, choosing a suitable
. However, choosing a suitable 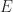 is more difficult than it might seem.
is more difficult than it might seem.
Consider the matrix
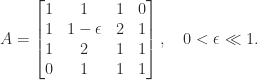
Since Cholesky factorization generates the same sequence of Schur complements as Gaussian elimination, it suffices to consider Gaussian elimination. The diagonal elements of 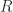 are the square roots of the pivots. After one step of elimination the reduced matrix is
are the square roots of the pivots. After one step of elimination the reduced matrix is
![\notag A^{(2)} = \left[\begin{array}{c|ccc} 1 & 1 & 1 & 1\\\hline 0 & -\epsilon & 1 & 1\\ 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 1 \end{array}\right],](https://s0.wp.com/latex.php?latex=%5Cnotag+++A%5E%7B%282%29%7D+%3D+++%5Cleft%5B%5Cbegin%7Barray%7D%7Bc%7Cccc%7D++++1+%26+1++++++++++%26+1+%26+1%5C%5C%5Chline++++0+%26+-%5Cepsilon+%26++1+++%26+1%5C%5C++++0+%26++1++++++++++%26+0+%26+1%5C%5C++++0+%26+++1+++++++++%26+1+%26+1+++%5Cend%7Barray%7D%5Cright%5D%2C+&bg=ffffff&fg=222222&s=0&c=20201002)
and the trailing 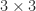 matrix (a Schur complement) is clearly indefinite because the
matrix (a Schur complement) is clearly indefinite because the  entry, which is the next pivot, is negative. We can make the (2,2) entry positive by adding
entry, which is the next pivot, is negative. We can make the (2,2) entry positive by adding 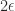 to it:
to it:
![\notag A^{(2)} + E = \left[\begin{array}{c|ccc} 1 & 1 & 1 & 1\\\hline 0 & \epsilon & 1 & 1\\ 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 1 \end{array}\right] \quad (E = 2 \mskip1mu\epsilon \mskip1mu e_2e_2^T).](https://s0.wp.com/latex.php?latex=%5Cnotag+++A%5E%7B%282%29%7D+%2B+E+%3D+++%5Cleft%5B%5Cbegin%7Barray%7D%7Bc%7Cccc%7D++++1+%26+1++++++++++%26+1+%26+1%5C%5C%5Chline++++0+%26+%5Cepsilon+%26+1+++%26+1%5C%5C++++0+%26+1+++++++++++%26+0+%26+1%5C%5C++++0+%26+1+++++++++++%26+1+%26+1+++%5Cend%7Barray%7D%5Cright%5D+++%5Cquad+++%28E+%3D++2+%5Cmskip1mu%5Cepsilon+%5Cmskip1mu+e_2e_2%5ET%29.+&bg=ffffff&fg=222222&s=0&c=20201002)
The next stage of the factorization can complete and it yields
![\notag A^{(3)} = \left[\begin{array}{cc|cc} 1 & 1 & 1 & 1 \\ 0 & \epsilon & 1 & 1 \\\hline\rule{0cm}{18pt} 0 & 0 & -\displaystyle\frac{1}{\epsilon} & 1 - \displaystyle\frac{1}{\epsilon}\\\rule{0cm}{20pt} 0 & 0 &1 - \displaystyle\frac{1}{\epsilon} & 1 - \displaystyle\frac{1}{\epsilon} \end{array}\right],](https://s0.wp.com/latex.php?latex=%5Cnotag+++A%5E%7B%283%29%7D+%3D+++%5Cleft%5B%5Cbegin%7Barray%7D%7Bcc%7Ccc%7D++++1+%26+1++++++++++%26+1+%26+1+%5C%5C++++0+%26+%5Cepsilon+++%26+1+%26+1+%5C%5C%5Chline%5Crule%7B0cm%7D%7B18pt%7D++++0+%26+0++++++++++%26+-%5Cdisplaystyle%5Cfrac%7B1%7D%7B%5Cepsilon%7D+%26+1+-+%5Cdisplaystyle%5Cfrac%7B1%7D%7B%5Cepsilon%7D%5C%5C%5Crule%7B0cm%7D%7B20pt%7D++++0+%26+0++++++++++%261+-+%5Cdisplaystyle%5Cfrac%7B1%7D%7B%5Cepsilon%7D+%26++1+-+%5Cdisplaystyle%5Cfrac%7B1%7D%7B%5Cepsilon%7D+++%5Cend%7Barray%7D%5Cright%5D%2C+&bg=ffffff&fg=222222&s=0&c=20201002)
The trailing 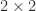 submatrix has elements of order
submatrix has elements of order 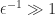 . Not only will a perturbation of order
. Not only will a perturbation of order 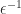 be required to the
be required to the 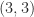 element to allow the Cholesky factorization to continue, but the Cholesky factor will have elements of order
element to allow the Cholesky factorization to continue, but the Cholesky factor will have elements of order 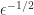 so numerical stability will likely be lost. Yet the smallest eigenvalue of
so numerical stability will likely be lost. Yet the smallest eigenvalue of 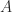 is of order
is of order  , so it should have been possible to make only an
, so it should have been possible to make only an  perturbation to
perturbation to 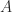 in order for the factorization to succeed.
in order for the factorization to succeed.
This example shows that if we are to increase a pivot element then we need a more sophisticated strategy that takes account of the size of the resulting elements of the factors and the effect on later stages of the factorization.
A modified Cholesky factorization should satisfy, as far as possible, four objectives.
Gill and Murray (1974) gave the first modified Cholesky algorithm, which computes 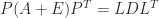 with diagonal
with diagonal 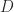 and
and 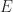 . It was refined by Gill, Murray, and Wright in 1981. Schnabel and Eskow (1990) gave an algorithm that attempts to produce smaller values of
. It was refined by Gill, Murray, and Wright in 1981. Schnabel and Eskow (1990) gave an algorithm that attempts to produce smaller values of 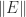 , partly by exploiting eigenvalue bounds obtained from Gershgorin’s theorem. That algorithm was subsequently improved by Schnabel and Eskow (1999).
, partly by exploiting eigenvalue bounds obtained from Gershgorin’s theorem. That algorithm was subsequently improved by Schnabel and Eskow (1999).
A different approach was taken by Cheng and Higham (1998), building on an earlier idea by Bunch and Sorensen. This approach computes a block 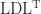 factorization
factorization  , were
, were 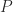 is a permutation matrix,
is a permutation matrix, 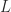 is unit lower triangular, and
is unit lower triangular, and 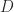 is block diagonal with diagonal blocks of size
is block diagonal with diagonal blocks of size  or
or 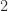 . The pivoting strategy is the symmetric rook pivoting strategy of Ashcraft, Grimes, and Lewis (1998), which has the key property of producing a bounded
. The pivoting strategy is the symmetric rook pivoting strategy of Ashcraft, Grimes, and Lewis (1998), which has the key property of producing a bounded 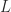 factor. The cost of pivoting is typically
factor. The cost of pivoting is typically 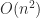 comparisons but can be as large as
comparisons but can be as large as  in the worst case. Cheng and Higham compute the perturbation
in the worst case. Cheng and Higham compute the perturbation 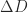 of minimal Frobenius norm such that
of minimal Frobenius norm such that 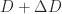 has eigenvalues greater than or equal to
has eigenvalues greater than or equal to 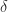 , where
, where 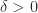 is a parameter. The modified Cholesky factorization is then
is a parameter. The modified Cholesky factorization is then 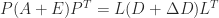 .
.
A significant advantage of the block  approach is that it is modular: any implementation of the factorization can be used and the modification is simply inexpensive postprocessing of the
approach is that it is modular: any implementation of the factorization can be used and the modification is simply inexpensive postprocessing of the 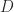 factor. The other algorithms are not simple modifications of an
factor. The other algorithms are not simple modifications of an 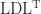 factorization and are not straightforward to implement in an efficient way as a block algorithm. Note that in the block
factorization and are not straightforward to implement in an efficient way as a block algorithm. Note that in the block 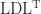 approach
approach 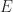 is a full matrix and it is not explicitly computed.
is a full matrix and it is not explicitly computed.
Modified Cholesky software is not widely available in libraries. Implementations of the Cheng–Higham algorithm are available in
Example
We take the  matrix above with
matrix above with 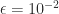 :
:
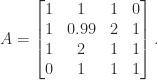
It has eigenvalues
-1.0050e+00 -2.3744e-01 1.0000e+00 4.2325e+00
The Gill–Murray–Wright algorithm computes as 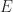 the diagonal matrix with diagonal elements
the diagonal matrix with diagonal elements
0 2.0200e+00 2.0000e+00 0
while the Schnabel–Eskow algorithm (1999) computes 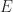 with diagonal elements
with diagonal elements
1.0000e+00 1.0050e+00 1.0050e+00 1.0000e+00
For the Cheng–Higham algorithm with 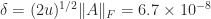 (where
(where  is the unit roundoff), the perturbed matrix
is the unit roundoff), the perturbed matrix  is
is
1.0000e+00 1.0000e+00 1.0000e+00 0
1.0000e+00 1.4950e+00 1.4975e+00 9.9749e-01
1.0000e+00 1.4975e+00 1.5000e+00 1.0025e+00
0 9.9749e-01 1.0025e+00 2.0100e+00
The Frobenius norms of the perturbations to 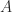 are
are 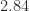 ,
,  , and
, and 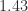 , respectively, and the 2-norm condition numbers are
, respectively, and the 2-norm condition numbers are 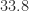 ,
, 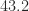 , and
, and  . The large condition number for the Cheng–Higham algorithm is caused by the value of the parameter
. The large condition number for the Cheng–Higham algorithm is caused by the value of the parameter 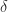 . With
. With 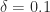 , the perturbed matrix is
, the perturbed matrix is
1.0000e+00 1.0000e+00 1.0000e+00 0
1.0000e+00 1.5453e+00 1.4475e+00 9.9724e-01
1.0000e+00 1.4475e+00 1.5497e+00 1.0027e+00
0 9.9724e-01 1.0027e+00 2.1100e+00
at Frobenius norm distance  from
from 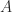 and with
and with 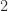 -norm condition number
-norm condition number 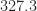 . For comparison, the symmetric matrix with all eigenvalues greater than or equal to
. For comparison, the symmetric matrix with all eigenvalues greater than or equal to  that is closest to
that is closest to 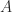 in the Frobenius norm is at a distance
in the Frobenius norm is at a distance 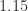 from
from 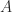 .
.
In general, there is no clear ordering of the different modified Cholesky methods in terms of their ability to satisfy the four criteria.
References
This is a minimal set of references, which contain further useful references within.
- Sheung Hun Cheng and Nicholas Higham, A Modified Cholesky Algorithm Based on a Symmetric Indefinite Factorization, SIAM J. Matrix Anal. Appl. 19(4), 1097–1110, 1998.
- Haw-Ren Fang and Dianne O’Leary, Modified Cholesky Algorithms: A Catalog with New Approaches, Math. Program. 115, 319–349, 2008
- Philip Gill, Walter Murray, and Margaret Wright, Practical Optimization, Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, 2020. Republication of book first published by Academic Press, 1981.
- Thomas McSweeney, Modified Cholesky Decomposition and Applications, M.Sc. Thesis, The University of Manchester, 2017.
- Robert Schnabel and Elizabeth Eskow, A Revised Modified Cholesky Factorization Algorithm, SIAM J. Optim. 9(4), 1135–1148, 1999.

