I thought it would be useful to provide my own MATLAB function nearcorr.m implementing the alternating projections algorithm. The listing is below. To see how it compares with the NAG code g02aa.m I ran the test code
%NEARCORR_TEST Compare g02aa and nearcorr.
rng(10) % Seed random number generators.
n = 100;
A = gallery('randcorr',n); % Random correlation matrix.
E = randn(n)*1e-1; A = A + (E + E')/2; % Perturb it.
tol = 1e-10;
% A = cor1399; tol = 1e-4;
fprintf('g02aa:\n')
maxits = int64(-1); % For linear equation solver.
maxit = int64(-1); % For Newton iteration.
tic
[~,X1,iter1,feval,nrmgrd,ifail] = g02aa(A,'errtol',tol,'maxits',maxits, ...
'maxit',maxit);
toc
fprintf(' Newton steps taken: %d\n', iter1);
fprintf(' Norm of gradient of last Newton step: %6.4f\n', nrmgrd);
if ifail > 0, fprintf(' g02aa failed with ifail = %g\n', ifail), end
fprintf('nearcorr:\n')
tic
[X2,iter2] = nearcorr(A,tol,[],[],[],[],1);
toc
fprintf(' Number of iterations: %d\n', iter2);
fprintf(' Normwise relative difference between computed solutions:')
fprintf('%9.2e\n', norm(X1-X2,1)/norm(X1,1))
Running under Windows 7 on an Ivy Bridge Core i7 processor @4.4Ghz I obtained the following results, where the “real-life” matrix is based on stock data:
| Matrix |
Code |
Time (secs) |
Iterations |
| 1. Random (100), tol = 1e-10 |
g02aa |
0.023 |
4 |
|
nearcorr |
0.052 |
15 |
| 2. Random (500), tol = 1e-10 |
g02aa |
0.48 |
4 |
|
nearcorr |
3.01 |
26 |
| 3. Real-life (1399), tol = 1e-4 |
g02aa |
6.8 |
5 |
|
nearcorr |
100.6 |
68 |
The results show that while nearcorr can be fast for small dimensions, the number of iterations, and hence its run time, tends to increase with the dimension and it can be many times slower than the Newton method. This is a stark illustration of the difference between quadratic convergence and linear (with problem-dependent constant) convergence. Here is my MATLAB function nearcorr.m.
function [X,iter] = nearcorr(A,tol,flag,maxits,n_pos_eig,w,prnt)
%NEARCORR Nearest correlation matrix.
% X = NEARCORR(A,TOL,FLAG,MAXITS,N_POS_EIG,W,PRNT)
% finds the nearest correlation matrix to the symmetric matrix A.
% TOL is a convergence tolerance, which defaults to 16*EPS.
% If using FLAG == 1, TOL must be a 2-vector, with first component
% the convergence tolerance and second component a tolerance
% for defining "sufficiently positive" eigenvalues.
% FLAG = 0: solve using full eigendecomposition (EIG).
% FLAG = 1: treat as "highly non-positive definite A" and solve
% using partial eigendecomposition (EIGS).
% MAXITS is the maximum number of iterations (default 100, but may
% need to be increased).
% N_POS_EIG (optional) is the known number of positive eigenvalues of A.
% W is a vector defining a diagonal weight matrix diag(W).
% PRNT = 1 for display of intermediate output.
% By N. J. Higham, 13/6/01, updated 30/1/13, 15/11/14, 07/06/15.
% Reference: N. J. Higham, Computing the nearest correlation
% matrix---A problem from finance. IMA J. Numer. Anal.,
% 22(3):329-343, 2002.
if ~isequal(A,A'), error('A must by symmetric.'), end
if nargin < 2 || isempty(tol), tol = length(A)*eps*[1 1]; end
if nargin < 3 || isempty(flag), flag = 0; end
if nargin < 4 || isempty(maxits), maxits = 100; end
if nargin < 6 || isempty(w), w = ones(length(A),1); end
if nargin < 7, prnt = 1; end
n = length(A);
if flag >= 1
if nargin < 5 || isempty(n_pos_eig)
[V,D] = eig(A); d = diag(D);
n_pos_eig = sum(d >= tol(2)*d(n));
end
if prnt, fprintf('n = %g, n_pos_eig = %g\n', n, n_pos_eig), end
end
X = A; Y = A;
iter = 0;
rel_diffX = inf; rel_diffY = inf; rel_diffXY = inf;
dS = zeros(size(A));
w = w(:); Whalf = sqrt(w*w');
while max([rel_diffX rel_diffY rel_diffXY]) > tol(1)
Xold = X;
R = Y - dS;
R_wtd = Whalf.*R;
if flag == 0
X = proj_spd(R_wtd);
elseif flag == 1
[X,np] = proj_spd_eigs(R_wtd,n_pos_eig,tol(2));
end
X = X ./ Whalf;
dS = X - R;
Yold = Y;
Y = proj_unitdiag(X);
rel_diffX = norm(X-Xold,'fro')/norm(X,'fro');
rel_diffY = norm(Y-Yold,'fro')/norm(Y,'fro');
rel_diffXY = norm(Y-X,'fro')/norm(Y,'fro');
iter = iter + 1;
if prnt
fprintf('%2.0f: %9.2e %9.2e %9.2e', ...
iter, rel_diffX, rel_diffY, rel_diffXY)
if flag >= 1, fprintf(' np = %g\n',np), else fprintf('\n'), end
end
if iter > maxits
error(['Stopped after ' num2str(maxits) ' its. Try increasing MAXITS.'])
end
end
%%%%%%%%%%%%%%%%%%%%%%%%
function A = proj_spd(A)
%PROJ_SPD
if ~isequal(A,A'), error('Not symmetric!'), end
[V,D] = eig(A);
A = V*diag(max(diag(D),0))*V';
A = (A+A')/2; % Ensure symmetry.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [A,n_pos_eig_found] = proj_spd_eigs(A,n_pos_eig,tol)
%PROJ_SPD_EIGS
if ~isequal(A,A'), error('Not symmetric!'), end
k = n_pos_eig + 10; % 10 is safety factor.
if k > length(A), k = n_pos_eig; end
opts.disp = 0;
[V,D] = eigs(A,k,'LA',opts); d = diag(D);
j = (d > tol*max(d));
n_pos_eig_found = sum(j);
A = V(:,j)*D(j,j)*V(:,j)'; % Build using only the selected eigenpairs.
A = (A+A')/2; % Ensure symmetry.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function A = proj_unitdiag(A)
%PROJ_SPD
n = length(A);
A(1:n+1:n^2) = 1;
Updates
- Links updated August 4, 2014.
nearcorr.m corrected November 15, 2014: iter was incorrectly initialized (thanks to Mike Croucher for pointing this out).- Added link to Mike Croucher’s Python alternating directions code, November 17, 2014.
- Corrected an error in the convergence test, June 7, 2015. Effect on performance will be minimal (thanks to Nataša Strabić for pointing this out).

. The Gershgorin discs for an
matrix
are the
discs in the complex plane defined by
lie in the union of the discs.
th Gershgorin disc is
and the closer
is to
the smaller the radius of the disc, so the discs are nested, with the disc corresponding to
containing all the others.
, so the centers of the discs are roughly equally spaced and shrink as the centers move to the right.
. The black dots are the eigenvalues. Here is the plot for
. The function used to produce these plots is
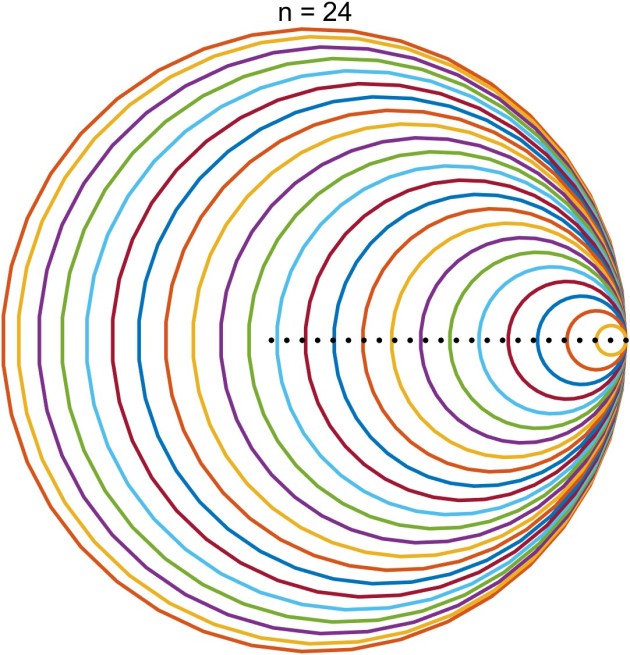 Here are two other matrices whose Gershgorin discs make a graphically interesting plot.
Here are two other matrices whose Gershgorin discs make a graphically interesting plot.





