One of the joys of is that it makes it so easy to typeset tables. I’ve created many
tables and I’ve always taken care to fine-tune them, most often by inserting commands of the form
\rule{0cm}{8pt} to stop superscripts hitting a horizontal rule in the line above.
I’ve been aware for a while of a package called booktabs that claims to produce more beautiful tables that more closely resemble those used in traditional typesetting. I was dissuaded from trying it by three things: the results looked rather spread out, the package discourages the use of vertical rules (which I thought I needed), and I wasn’t sure if publishers such as SIAM would allow it to be used in their journals.
I was encouraged to give booktabs a try while I was preparing the third edition of Handbook of Writing for the Mathematical Sciences. I redid the tables from the previous edition using the package and, after some experimentation, became convinced that booktabs is indeed a great aid to producing better tables.
The best way to illustrate the attractions of booktabs is with a simple example. This table is from a 2017 SIAM J. Sci. Comput. paper of which I am a co-author: 
The original table did not have the vertical rules at the sides or the horizontal rule at the bottom, but I have added them since many people include them.
Here is a revised version of the table created with booktabs:
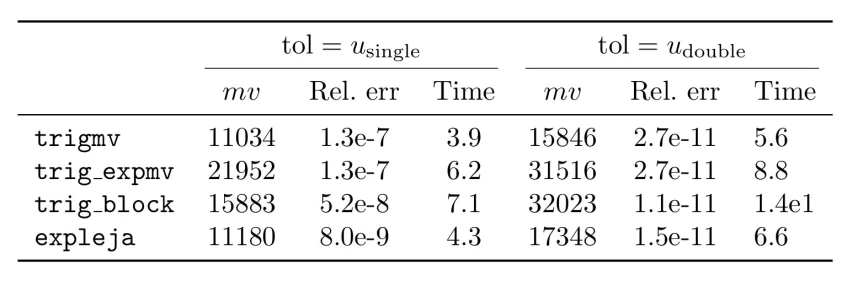
The second table dispenses with all the vertical rules and adds two partial horizontal rules to demarcate the span of the pairs of columns covered by the two tol values. Notice the thicker rules at the top and bottom and the greater spacing between lines. The booktabs version of the table is more aesthetically pleasing. It is also slightly easier to typeset. The rules at the top, middle, and bottom are typed with \toprule, \midrule, and \botomrule. The subrules are typed with \cmidrule{m-n} to span columns m to n. The usage \cmidrule(lr){m-n} crops (on the left and right) the rules so that adjacent subrules do not merge.
Here is the source code for the two tables:
% First version of table.
\begin{tabular}{|l|c|c|c|c|c|l|}\hline
& \multicolumn{3}{c|}{$\tol=\tols$} & \multicolumn{3}{c|}{$\tol=\told$}\\
& $mv$ & Rel.~err & Time & $mv$ & Rel.~err & Time \\\hline
\trigmv & 11034 & 1.3e-7 & 3.9 & 15846 & 2.7e-11 & 5.6 \\
\trigexpmv & 21952 & 1.3e-7 & 6.2 & 31516 & 2.7e-11 & 8.8 \\
\trigblock & 15883 & 5.2e-8 & 7.1 & 32023 & 1.1e-11 & 1.4e1\\
\expleja & 11180 & 8.0e-9 & 4.3 & 17348 & 1.5e-11 & 6.6 \\\hline
\end{tabular}
% Second version of table, with booktabs.
\begin{tabular}{lcccccl}\toprule
& \multicolumn{3}{c}{$\tol=\tols$} & \multicolumn{3}{c}{$\tol=\told$}
\\\cmidrule(lr){2-4}\cmidrule(lr){5-7}
& $mv$ & Rel.~err & Time & $mv$ & Rel.~err & Time\\\midrule
\trigmv & 11034 & 1.3e-7 & 3.9 & 15846 & 2.7e-11 & 5.6 \\
\trigexpmv & 21952 & 1.3e-7 & 6.2 & 31516 & 2.7e-11 & 8.8 \\
\trigblock & 15883 & 5.2e-8 & 7.1 & 32023 & 1.1e-11 & 1.4e1\\
\expleja & 11180 & 8.0e-9 & 4.3 & 17348 & 1.5e-11 & 6.6 \\\bottomrule
\end{tabular}
Despite my initial skepticism, it does seem possible to manage without vertical rules in tables. Indeed, the Chicago Manual of Style (17th edition, 2017) advises that “Vertical rules should be used sparingly—for example, when a table is doubled up … or as an aid to comprehension in an especially long or complex table”. The extra space that booktabs puts around horizontal rules makes the table nicer to look at and helps to avoid the problem of superscripts hitting the rule above. And, importantly, SIAM are happy to for authors to use booktabs in their papers.
I am now using booktabs in all my code.
For more before-and-after examples of tables, which illustrate table design as well as the use of booktabs, see Handbook of Writing for the Mathematical Sciences (third edition, 2020).
One booktab tip that I needed in producing the Handbook was to reduce the space at the edges of some of the widest tables by shortening the horizontal rules. This can be done by putting @{} at the beginning and end of the column formatting argument. For the example above, this is done with
\begin{tabular}{@{}lcccccl@{}}\toprule
This blog contains various other posts about .


