What Is the Numerical Range of a Matrix?

The numerical range of a matrix A\in\mathbb{C}^{n\times n}, also known as the field of values, is the set of complex numbers

W(A) = \biggl\{\, \displaystyle\frac{z^*Az}{z^*z}: 0\ne z\in\mathbb{C}^n \,\biggr\}.

The set W(A) is compact and convex (a nontrivial property proved by Toeplitz and Hausdorff), and it contains all the eigenvalues of A. For normal matrices it is the convex hull of the eigenvalues. For a Hermitian matrix, W(A) is a segment of the real axis, while for a skew-Hermitian matrix it is a segment of the imaginary axis.

The following figure plots in blue the boundaries of the the numerical ranges of nine 16\times 16 matrices, with the eigenvalues shown as black dots. They were plotted using the function fv in the Matrix Computation Toolbox. The matrices are from Anymatrix.

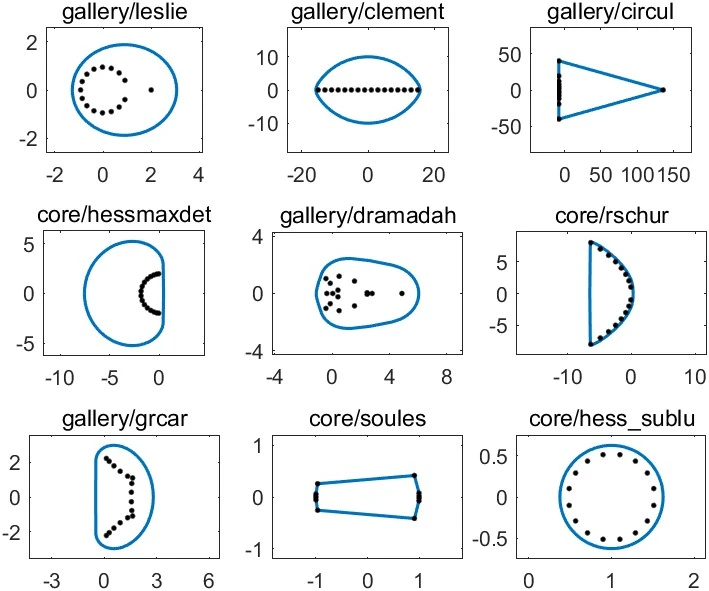
fov_plots.jpg

A method for computing the boundary of the numerical range is based on the observation that for any z\in\mathbb{C},

\notag z^*Az = \underbrace{z^* \frac{1}{2}(A+A^*) z}_{\mathrm{\phantom{1234}real\phantom{1234}}} + \underbrace{z^* \frac{1}{2}(A-A^*) z}_{\mathrm{pure~imaginary}} \qquad (1)

This implies that the real part of z^*Az/z^*z lies between the largest and smallest eigenvalues of the Hermitian matrix (A+A^*)/2, which define a vertical strip in which the numerical range lies. Since W(\mathrm{e}^{\mathrm{i}\theta} A) = \mathrm{e}^{\mathrm{i}\theta} W(A), we can apply the same reasoning to the rotated matrix A(\theta) = \mathrm{e}^{\mathrm{i}\theta} A, and taking a range of \theta\in[0,\pi] we obtain an approximation the boundary of the numerical range.

The quantity

\notag \omega(A) = \max \bigl\{\, \mathrm{Re}\, w : w \in W(A) \,\bigr\}

is called the numerical abscissa, and by (1), \omega(A) is the largest eigenvalue of the Hermitian matrix (A+A^*)/2. The numerical abscissa determines the rate of growth of \|\mathrm{e}^{tA}\| for small positive t.

Associated with the numerical range is the numerical radius

\notag r(A) = \max\{\, |w| : w \in W(A) \,\}.

Note that r(A^*) = r(A). Also, r(A) \ge \rho(A), where \rho is the spectral radius (the largest absolute value of any eigenvalue), since W(A) contains the eigenvalues of A.

The numerical radius differs by at most a factor 2 from the 2-norm:

\notag \frac{1}{2} \|A\|_2 \le r(A) \le \|A\|_2. \qquad (2)

When A is normal, r(A) = \|A\|_2.

The numerical radius is a matrix norm, but not a consistent norm (that is, r(AB) \le r(A)r(B) does not hold in general). However, it is it true that

\notag r(A^k) \le r(A)^k, \quad k\ge 1.

Combining this with with the lower bound in (2) gives

\notag \|A^k\|_2 \le 2 r(A)^k, \quad k \ge 1,

so if we know r(A) then we can bound \|A^k\|_2 for all k.

The numerical radius can be characterized as the solution of an optimization problem over the Hermitian matrices:

\notag r(A) = - \max\biggl\{\, \lambda_{\min}\biggl( \begin{bmatrix} Z\!\! & A \\ A^*\!\! & -Z \end{bmatrix} \biggr): Z=Z^*\in\mathbb{C}^{n\times n} \,\biggr\}.

Notes and References

For proofs of the results given here see Horn and Johnson (2013) or Horn and Johnson (1991), and see the latter for details of the algorithm for computing the numerical range. See Benzi (2020) for a discussion of applications of the numerical range in numerical analysis.

Related Blog Posts

This article is part of the “What Is” series, available from https://nhigham.com/category/what-is and in PDF form from the GitHub repository https://github.com/higham/what-is.

Leave a comment