What Is a Modified Cholesky Factorization?

Newton methods for minimizing a function $F:\mathbb{R}^n \to \mathbb{R}$ generate a sequence of points $x_k$ , where the step from $x_k$ to $x_{k+1}$ is along a search direction $p_k$ determined from a linear system $G_k p_k = -g_k$ , where $g_k = \nabla F(x_k)$ is the gradient and $G_k$ is an approximation to the Hessian matrix $\nabla^2 F(x_k)$ . The equation $g_k^Tp_k = - p_k^T G_k p_k$ shows that $G_k$ is a descent direction if $p_k^T G_k p_k > 0$ , and in order to guarantee that this condition holds for all $p_k$ we need $G_k$ to be positive definite. But even if $G_k$ is the exact Hessian, positive definiteness is not guaranteed far from a minimizer. We can modify the method to ensure definiteness of $G_k$ , as with quasi-Newton methods. Or we can perturb the matrix, if necessary, to make it positive definite. Modified Cholesky factorization perturbs and factorizes the matrix at the same time. It is useful in other situations, too, such as in constructing preconditioners and in bounding the distance to a positive semidefinite matrix.

A modified Cholesky factorization of a symmetric matrix $A$ is a factorization $P(A + E)P^T = LDL^T$ , where $P$ is a permutation matrix, $L$ is unit lower triangular, and $D$ is diagonal or block diagonal and positive definite. It follows that $A+E$ is a positive definite matrix.

A natural way to compute a modified Cholesky factorization is to modify the Cholesky factorization algorithm. Cholesky factorization fails when it tries to take the square root of a negative quantity or divide by zero. We can avoid both possibilities by increasing nonpositive pivots when they are encountered. This corresponds to making a diagonal perturbation $E$ to $A$ and computing a Cholesky factorization $A + E = R^T\!R$ . However, choosing a suitable $E$ is more difficult than it might seem.

Consider the matrix

$\notag A = \begin{bmatrix} 1 & 1 & 1 & 0 \\ 1 & 1-\epsilon & 2 & 1\\ 1 & 2 & 1 & 1\\ 0 & 1 & 1 & 1 \end{bmatrix}, \quad 0 < \epsilon \ll 1.$

Since Cholesky factorization generates the same sequence of Schur complements as Gaussian elimination, it suffices to consider Gaussian elimination. The diagonal elements of $R$ are the square roots of the pivots. After one step of elimination the reduced matrix is

$\notag A^{(2)} = \left[\begin{array}{c|ccc} 1 & 1 & 1 & 1\\\hline 0 & -\epsilon & 1 & 1\\ 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 1 \end{array}\right],$

and the trailing $3\times 3$ matrix (a Schur complement) is clearly indefinite because the $(2,2)$ entry, which is the next pivot, is negative. We can make the (2,2) entry positive by adding $2\epsilon$ to it:

$\notag A^{(2)} + E = \left[\begin{array}{c|ccc} 1 & 1 & 1 & 1\\\hline 0 & \epsilon & 1 & 1\\ 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 1 \end{array}\right] \quad (E = 2 \mskip1mu\epsilon \mskip1mu e_2e_2^T).$

The next stage of the factorization can complete and it yields

$\notag A^{(3)} = \left[\begin{array}{cc|cc} 1 & 1 & 1 & 1 \\ 0 & \epsilon & 1 & 1 \\\hline\rule{0cm}{18pt} 0 & 0 & -\displaystyle\frac{1}{\epsilon} & 1 - \displaystyle\frac{1}{\epsilon}\\\rule{0cm}{20pt} 0 & 0 &1 - \displaystyle\frac{1}{\epsilon} & 1 - \displaystyle\frac{1}{\epsilon} \end{array}\right],$

The trailing $2\times 2$ submatrix has elements of order $\epsilon^{-1} \gg 1$ . Not only will a perturbation of order $\epsilon^{-1}$ be required to the $(3,3)$ element to allow the Cholesky factorization to continue, but the Cholesky factor will have elements of order $\epsilon^{-1/2}$ so numerical stability will likely be lost. Yet the smallest eigenvalue of $A$ is of order $1$ , so it should have been possible to make only an $O(1)$ perturbation to $A$ in order for the factorization to succeed.

This example shows that if we are to increase a pivot element then we need a more sophisticated strategy that takes account of the size of the resulting elements of the factors and the effect on later stages of the factorization.

A modified Cholesky factorization should satisfy, as far as possible, four objectives.

If $A$ is “sufficiently positive definite” then $E$ is zero.
If $A$ is indefinite, $\|E\|$ is not much larger than
$\notag \min \{\, \|\Delta A\| : A+\Delta A~ \text{is positive semidefinite} \,\}$

for some appropriate norm.
The matrix $A+E$ is reasonably well conditioned.
The cost of the algorithm is the same as the cost of standard Cholesky factorization, that is, $n^3/3 + O(n^2)$ flops for an $n\times n$ matrix.

Gill and Murray (1974) gave the first modified Cholesky algorithm, which computes $P(A + E)P^T = LDL^T$ with diagonal $D$ and $E$ . It was refined by Gill, Murray, and Wright in 1981. Schnabel and Eskow (1990) gave an algorithm that attempts to produce smaller values of $\|E\|$ , partly by exploiting eigenvalue bounds obtained from Gershgorin’s theorem. That algorithm was subsequently improved by Schnabel and Eskow (1999).

A different approach was taken by Cheng and Higham (1998), building on an earlier idea by Bunch and Sorensen. This approach computes a block $\mathrm{LDL^T}$ factorization $PAP^T = LDL^T$ , were $P$ is a permutation matrix, $L$ is unit lower triangular, and $D$ is block diagonal with diagonal blocks of size $1$ or $2$ . The pivoting strategy is the symmetric rook pivoting strategy of Ashcraft, Grimes, and Lewis (1998), which has the key property of producing a bounded $L$ factor. The cost of pivoting is typically $O(n^2)$ comparisons but can be as large as $O(n^3)$ in the worst case. Cheng and Higham compute the perturbation $\Delta D$ of minimal Frobenius norm such that $D + \Delta D$ has eigenvalues greater than or equal to $\delta$ , where $\delta > 0$ is a parameter. The modified Cholesky factorization is then $P(A+E)P^T = L(D+\Delta D)L^T$ .

A significant advantage of the block $\mathrm{LDL^T}$ approach is that it is modular: any implementation of the factorization can be used and the modification is simply inexpensive postprocessing of the $D$ factor. The other algorithms are not simple modifications of an $\mathrm{LDL^T}$ factorization and are not straightforward to implement in an efficient way as a block algorithm. Note that in the block $\mathrm{LDL^T}$ approach $E$ is a full matrix and it is not explicitly computed.

Modified Cholesky software is not widely available in libraries. Implementations of the Cheng–Higham algorithm are available in

the NAG Library routine f01mdf (real_modified_cholesky),
the MATLAB codes in the repository https://github.com/higham/modified-cholesky.

Example

We take the $4\times 4$ matrix above with $\epsilon = 10^{-2}$ :

$\notag A = \begin{bmatrix} 1 & 1 & 1 & 0 \\ 1 & 0.99 & 2 & 1\\ 1 & 2 & 1 & 1\\ 0 & 1 & 1 & 1 \end{bmatrix}.$

It has eigenvalues

-1.0050e+00  -2.3744e-01   1.0000e+00   4.2325e+00

The Gill–Murray–Wright algorithm computes as $E$ the diagonal matrix with diagonal elements

0   2.0200e+00   2.0000e+00            0

while the Schnabel–Eskow algorithm (1999) computes $E$ with diagonal elements

1.0000e+00   1.0050e+00   1.0050e+00   1.0000e+00

For the Cheng–Higham algorithm with $\delta = (2u)^{1/2} \|A\|_F = 6.7 \times10^{-8}$ (where $u \approx 1.11 \times 10^{-16}$ is the unit roundoff), the perturbed matrix $A+E$ is

1.0000e+00   1.0000e+00   1.0000e+00            0
1.0000e+00   1.4950e+00   1.4975e+00   9.9749e-01
1.0000e+00   1.4975e+00   1.5000e+00   1.0025e+00
         0   9.9749e-01   1.0025e+00   2.0100e+00

The Frobenius norms of the perturbations to $A$ are $2.84$ , $2.00$ , and $1.43$ , respectively, and the 2-norm condition numbers are $33.8$ , $43.2$ , and $4.67 \times 10^8$ . The large condition number for the Cheng–Higham algorithm is caused by the value of the parameter $\delta$ . With $\delta = 0.1$ , the perturbed matrix is

1.0000e+00   1.0000e+00   1.0000e+00            0
1.0000e+00   1.5453e+00   1.4475e+00   9.9724e-01
1.0000e+00   1.4475e+00   1.5497e+00   1.0027e+00
         0   9.9724e-01   1.0027e+00   2.1100e+00

at Frobenius norm distance $1.57$ from $A$ and with $2$ -norm condition number $327.3$ . For comparison, the symmetric matrix with all eigenvalues greater than or equal to $0.1$ that is closest to $A$ in the Frobenius norm is at a distance $1.15$ from $A$ .

In general, there is no clear ordering of the different modified Cholesky methods in terms of their ability to satisfy the four criteria.

References

This is a minimal set of references, which contain further useful references within.

Sheung Hun Cheng and Nicholas Higham, A Modified Cholesky Algorithm Based on a Symmetric Indefinite Factorization, SIAM J. Matrix Anal. Appl. 19(4), 1097–1110, 1998.
Haw-Ren Fang and Dianne O’Leary, Modified Cholesky Algorithms: A Catalog with New Approaches, Math. Program. 115, 319–349, 2008
Philip Gill, Walter Murray, and Margaret Wright, Practical Optimization, Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, 2020. Republication of book first published by Academic Press, 1981.
Thomas McSweeney, Modified Cholesky Decomposition and Applications, M.Sc. Thesis, The University of Manchester, 2017.
Robert Schnabel and Elizabeth Eskow, A Revised Modified Cholesky Factorization Algorithm, SIAM J. Optim. 9(4), 1135–1148, 1999.

What Is the Matrix Sign Function?

The matrix sign function is the matrix function corresponding to the scalar function of a complex variable

$\notag \mathrm{sign}(z) = \begin{cases} 1, & \mathop{\mathrm{Re}} z > 0, \\ -1, & \mathop{\mathrm{Re}} z < 0. \end{cases}$

Note that this function is undefined on the imaginary axis. The matrix sign function can be obtained from the Jordan canonical form definition of a matrix function: if $A = XJX^{-1}$ is a Jordan decomposition with $\mathrm{diag}(J) = \mathrm{diag}(\lambda_i)$ then

$\notag S = \mathrm{sign}(A) = X \mathrm{sign}(J)X^{-1} = X \mathrm{diag}(\mathrm{sign}(\lambda_i))X^{-1},$

since all the derivatives of the sign function are zero. The eigenvalues of $S$ are therefore all $\pm 1$ . Moreover, $S^2 = I$ , so $S$ is an involutory matrix.

The matrix sign function was introduced by Roberts in 1971 as a tool for model reduction and for solving Lyapunov and algebraic Riccati equations. The fundamental property that Roberts employed is that $(I+S)/2$ and $(I-S)/2$ are projectors onto the invariant subspaces associated with the eigenvalues of $A$ in the open right-half plane and open left-half plane, respectively. Indeed without loss of generality we can assume that the eigenvalues of $A$ are ordered so that $J = \mathrm{diag}(J_1,J_2)$ , with the eigenvalues of $J_1\in\mathbb{C}^{p\times p}$ in the open left half-plane and those of $J_2\in\mathbb{C}^{q\times q}$ in the open right half-plane ( $p + q = n$ ). Then

$\notag S = X \begin{bmatrix} -I_p & 0 \\ 0 & I_q \end{bmatrix}X^{-1}$

and, writing $X = [X_1~X_2]$ , where $X_1$ is $n\times p$ and $X_2$ is $n\times q$ , we have

$\notag \begin{aligned} \displaystyle\frac{I+S}{2} &= X \begin{bmatrix} 0 & 0 \\ 0 & I_q \end{bmatrix}X^{-1} = X_2 X^{-1}(p+1\colon n,:),\\[\smallskipamount] \displaystyle\frac{I-S}{2} &= X \begin{bmatrix} I_p & 0 \\ 0 & 0 \end{bmatrix}X^{-1} = X_1 X^{-1}(1\colon p,:). \end{aligned}$

Also worth noting are the integral representation

$\notag \mathrm{sign}(A) = \displaystyle\frac{2}{\pi} A \int_0^{\infty} (t^2I+A^2)^{-1} \,\mathrm{d}t$

and the concise formula

$\notag \mathrm{sign}(A) = A (A^2)^{-1/2}.$

Application to Sylvester Equation

To see how the matrix sign function can be used, consider the Sylvester equation

$\notag AX - XB = C, \quad A \in \mathbb{C}^{m\times m}, \; B \in \mathbb{C}^{n\times n}, \; C \in \mathbb{C}^{m\times n}.$

This equation is the $(1,2)$ block of the equation

$\notag \begin{bmatrix} A & -C \\ 0 & B \end{bmatrix} = \begin{bmatrix} I_m & X \\ 0 & I_n \end{bmatrix} \begin{bmatrix} A & 0 \\ 0 & B \end{bmatrix} \begin{bmatrix} I_m & X \\ 0 & I_n \end{bmatrix}^{-1}.$

If $\mathrm{sign}(A) = I$ and $\mathrm{sign}(B) = -I$ then

$\notag \mathrm{sign} \left( \begin{bmatrix} A & -C \\ 0 & -B \end{bmatrix} \right) = \begin{bmatrix} I_m & X \\ 0 & I_n \end{bmatrix} \begin{bmatrix} I_m & 0 \\ 0 & -I_n \end{bmatrix} \begin{bmatrix} I_m & -X \\ 0 & I_n \end{bmatrix} = \begin{bmatrix} I_m & -2X \\ 0 & -I_n \end{bmatrix},$

so the solution $X$ can be read from the $(1,2)$ block of the sign of the block upper triangular matrix $\bigl[\begin{smallmatrix}A & -C\\ 0& B \end{smallmatrix}\bigr]$ . The conditions that $\mathrm{sign}(A)$ and $\mathrm{sign}(B)$ are identity matrices are satisfied for the Lyapunov equation $AX + XA^* = C$ when $A$ is positive stable, that is, when the eigenvalues of $A$ lie in the open right half-plane.

A generalization of this argument shows that the matrix sign function can be used to solve the algebraic Riccati equation $XFX - A^*X - XA - G = 0$ , where $F$ and $G$ are Hermitian.

Application to the Eigenvalue Problem

It is easy to see that $S = \mathrm{sign}(A)$ satisfies $\mathrm{trace}(S) = \mathrm{trace}(\mathrm{diag}(\mathrm{sign}(\lambda_i))) = q - p$ , where $p$ and $q$ are the number of eigenvalues in the open left-half plane and open right-half plane, respectively (as above). Since $n = p + q$ , we have the formulas

$\notag p = \displaystyle\frac{n - \mathrm{trace}(S)}{2}, \quad q = \displaystyle\frac{n + \mathrm{trace}(S)}{2}.$

More generally, for real $a$ and $b$ with $a < b$ ,

$\notag \displaystyle\frac{1}{2} \bigl( \mathrm{sign}(A - aI) - \mathrm{sign}(A - bI) \bigr)$

is the number of eigenvalues lying in the vertical strip $\{\, z: \mathop{\mathrm{Re}}z \in(a,b)\,\}$ . Formulas also exist to count the number of eigenvalues in rectangles and more complicated regions.

Computing the Matrix Sign Function

What makes the matrix sign function so interesting and useful is that it can be computed directly without first computing eigenvalues or eigenvectore of 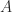$A$ . Roberts noted that the iteration

$\notag X_{k+1} = \displaystyle\frac{1}{2} (X_k + X_k^{-1}), \quad X_0 = A,$

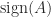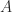converges quadratically to $\mathrm{sign}(A)$ . This iteration is Newton’s method applied to the equation $X^2 = I$ , with starting matrix $A$ . It is one of the rare circumstances in which explicitly inverting matrices is justified!

Various other iterations are available for computing 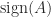$\mathrm{sign}(A)$ . A matrix multiplication-based iteration is the Newton–Schulz iteration

$\notag X_{k+1} = \displaystyle\frac{1}{2} X_k (3I - X_k^2), \quad X_0 = A.$

This iteration is quadratically convergent if $\|I-A^2\| < 1$ for some subordinate matrix norm. The Newton–Schulz iteration is the $[1/0]$ member of a Padé family of rational iterations

$X_{k+1} = X_k p_{\ell m}^{}\left(1-X_k^2\right) q_{\ell m}^{}\left(1-X_k^2\right)^{-1}, \quad X_0 = A,$

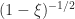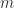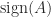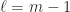where $p_{\ell m}(\xi)/q_{\ell m}(\xi)$ is the $[\ell/m]$ Padé approximant to $(1-\xi)^{-1/2}$ ( $p_{\ell m}$ and $q_{\ell m}$ are polynomials of degrees at most $\ell$ and $m$ , respectively). The iteration is globally convergent to $\mathrm{sign}(A)$ for $\ell = m-1$ and $\ell = m$ , and for $\ell \ge m+1$ it converges when $\|I-A^2\| < 1$ , with order of convergence $\ell+m+1$ in all cases.

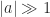Although the rate of convergence of these iterations is at least quadratic, and hence asymptotically fast, it can be slow initially. Indeed for $n = 1$ , if $|a| \gg 1$ then the Newton iteration computes 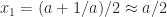$x_1 = (a+1/a)/2 \approx a/2$ , and so the early iterations make slow progress towards 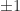$\pm 1$ . Fortunately, it is possible to speed up convergence with the use of scale parameters. The Newton iteration can be replaced by

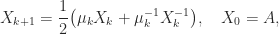
$\notag X_{k+1} = \displaystyle\frac{1}{2} \bigl(\mu_kX_k + \mu_k^{-1}X_k^{-1}\bigr), \quad X_0 = A,$

with, for example,

$\notag \mu_k = \sqrt{\|X_k^{-1}\|/\|X_k\|}.$

This parameter $\mu_k$ can be computed at no extra cost.

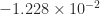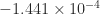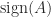As an example, we took A = gallery('lotkin',4), which has eigenvalues $1.887$ , $-1.980\times10^{-1}$ , $-1.228\times10^{-2}$ , and $-1.441\times10^{-4}$ to four significant figures. After six iterations of the unscaled Newton iteration $X_6$ had an eigenvalue $-100.8$ , showing that $X_6$ is far from $\mathrm{sign}(A)$ , which has eigenvalues 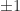$\pm 1$ . 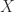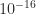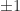Yet when scaled by $\mu_k$ (using the $1$ -norm), after six iterations all the eigenvalues of $X$ were within distance $10^{-16}$ of $\pm 1$ , and the iteration had converged to within this tolerance.

The Matrix Computation Toolbox contains a MATLAB function signm that computes the matrix sign function. It computes a Schur decomposition then obtains the sign of the triangular Schur factor by a finite recurrence. This function is too expensive for use in applications, but is reliable and is useful for experimentation.

Relation to Matrix Square Root and Polar Decomposition

The matrix sign function is closely connected with the matrix square root and the polar decomposition. This can be seen through the relations

$\notag \mathrm{sign}\left( \begin{bmatrix} 0 & A \\\ I & 0 \end{bmatrix} \right ) = \begin{bmatrix}0 & A^{1/2} \\ A^{-1/2} & 0 \end{bmatrix}, \\[\smallskipamount]$

for $A$ with no eigenvalues on the nonpositive real axis, and

$\notag \mathrm{sign}\left( \begin{bmatrix} 0 & A \\\ A^* & 0 \end{bmatrix} \right ) = \begin{bmatrix}0 & U \\ U^* & 0 \end{bmatrix},$

for nonsingular $A$ , where $A = UH$ is a polar decomposition. Among other things, these relations yield iterations for $A^{1/2}$ and $U$ by applying the iterations above to the relevant block $2n\times 2n$ matrix and reading off the (1,2) block.

References

This is a minimal set of references, which contain further useful references within.

Nicholas J. Higham, Functions of Matrices: Theory and Computation, Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, 2008. (Chapter 5.)
Charles Kenney and Alan Laub, Rational Iterative Methods for the Matrix Sign Function, SIAM J. Matrix Anal. Appl. 12(2), 273–291, 1991.
J. D. Roberts, Linear Model Reduction and Solution of the Algebraic Riccati Equation by Use of the Sign Function, Internat. J. Control 32, 677–687, 1980.

What Is a Fractional Matrix Power?

A $p$ th root of an $n\times n$ matrix $A$ is a matrix $X$ such that $X^p = A$ , and it can be written $X = A^{1/p}$ . For a rational number $r = j/k$ (where $j$ and $k$ are integers), defining $A^r$ is more difficult: is it $(A^j)^{1/k}$ or $(A^{1/k})^j$ ? These two possibilities can be different even for $n = 1$ . More generally, how can we define $A^\alpha$ for an arbitrary real number $\alpha$ ?

Recall, first, that for a nonzero complex scalar $z$ we define $z^\alpha = \mathrm{e}^{\alpha\log z}$ , where $\log$ is the principal logarithm: the one taking values in the strip $\{\, z : -\pi < \mathop{\mathrm{Im}} z \le \pi \,\}$ . We can generalize this definition to matrices. For a nonsingular matrix $A$ we define

$\notag A^\alpha = \mathrm{e}^{\alpha\log A}.$

Here the logarithm is the principal matrix logarithm, the matrix function built on the principal scalar logarithm, and so the eigenvalues of $\log A$ lie in the strip $\{\, z : -\pi < \mathop{\mathrm{Im}} z \le \pi \,\}$ . When $\alpha \in [-1,1]$ , the eigenvalues of $A^\alpha$ , which are $\lambda^\alpha$ where $\lambda$ is an eigenvalue of $A$ , lie in the segment $\{\, z: -|\alpha|\pi < \arg z \le |\alpha|\pi\,\}$ of the complex plane.

The most important special case is $\alpha = 1/p$ for a positive integer $p$ , in which case

$\notag A^{1/p} = \mathrm{e}^{\frac{1}{p}\log A}.$

We can check that

$\notag \bigl(A^{1/p}\bigr)^p = \bigl(\mathrm{e}^{\frac{1}{p}\log A}\bigr)^p = \mathrm{e}^{\log A} = A,$

so the definition does indeed produce a $p$ th root. The matrix $A^{1/p}$ is called the principal $p$ th root.

Returning to the case of rational $p$ , we note that

$\notag A^{j/k} = \mathrm{e}^{\frac{j}{k}\log A} = \Bigl(\mathrm{e}^{\frac{1}{k}\log A}\Bigr)^j = (A^{1/k})^j,$

but $(A^{j})^{1/k}$ can be a different matrix. In general, it is not true that $(A^\alpha)^\beta = (A^\beta)^\alpha$ for real $\alpha$ and $\beta$ , although for symmetric positive definite matrices this identity does hold because the eigenvalues are real and positive.

An integral expression for $A^\alpha$ valid for $\alpha \in(0,1)$ is

$\notag A^\alpha = \displaystyle\frac{\sin(\alpha\pi)} {\alpha\pi} A \int_0^{\infty}(t^{1/\alpha}I+A)^{-1}\,\mathrm{d}t, \quad \alpha \in(0,1).$

Another representation for $A = t (I - B)$ with $\rho(B) < 1$ is given by the binomial expansion

$\notag A^{\alpha} = t^{\alpha} \displaystyle\sum_{j=0}^\infty {\alpha \choose j}(-B)^j, \quad \rho(B) < 1.$

For $2\times 2$ real matrices of the form

$\notag A = \begin{bmatrix} a & b \\ c & a \end{bmatrix}$

with $bc < 0$ there is an explicit formula for $A^\alpha$ . It is easy to see that $A$ has eigenvalues $\lambda_{\pm} = a \pm \mathrm{i} d$ , where $d = (-bc)^{1/2}$ . Let $\theta = \arg(\lambda_+) \in (0,\pi)$ and $r = |\lambda_+|$ . It can be shown that

$\notag A^\alpha = \displaystyle\frac{r^\alpha}{d} \begin{bmatrix} d\cos(\alpha\theta) & b\sin(\alpha\theta) \\ c\sin(\alpha\theta) & d\cos(\alpha\theta) \end{bmatrix}.$

Computation

The formula $A^\alpha = \mathrm{e}^{\alpha \log A}$ can be used computationally, but it is somewhat indirect in that one must approximate both the exponential and the logarithm. A more direct algorithm based on the Schur decomposition and Padé approximation of the power function is developed by Higham and Lin (2013). MATLAB code is available from MathWorks File Exchange.

If $A$ is diagonalizable, so that $A = XDX^{-1}$ for some nonsingular $X$ with $D = \mathrm{diag}(\lambda_i)$ , then $A^\alpha = X D^\alpha X^{-1} = X \mathrm{diag}(\lambda_i^\alpha) X^{-1}$ . This formula is safe to use computationally only if $X$ is well conditioned. For defective (non-diagonalizable) $A$ we can express $A^\alpha$ in terms of the Jordan canonical form, but this expression is not useful computationally because the Jordan canonical form cannot be reliably computed.

Inverse Function

If $X = A^{1/2}$ then $A = X^2$ , by the definition of square root. If $X = A^{\alpha}$ does it follow that $A = X^{1/\alpha}$ ? Clearly, the answer is “no” in general because, for example, $X = A^2$ does not imply $A = X^{1/2}$ .

Using the matrix unwinding function it can be shown that $(A^{\alpha})^{1/\alpha} = A$ for $\alpha \in [-1,1]$ . Hence the function $g(A) = A^{1/\alpha}$ is the inverse function of $f(A) = A^{\alpha}$ for $\alpha\in[-1,1]$ .

Backward Error

How can we check the quality of an approximation $X$ to $A^{\alpha}$ ? For $\alpha = 1/p$ we can check the residual $A - X^p$ , but for real $p$ there is no natural residual. Instead we can look at the backward error.

For an approximation $X$ to $A^\alpha$ , a backward error is a matrix $\Delta A$ such that $X = (A + \Delta A)^\alpha$ . Assume that $A$ and $X$ are nonsingular and that $\alpha \in [-1,1]$ . Then, as shown in the previous section, $X = (A + \Delta A)^\alpha$ implies $\Delta A = X^{1/\alpha} - A$ . Hence the normwise relative backward error is

$\notag \eta(X) = \displaystyle\frac{ \|X^{1/\alpha} - A \|}{\|A\|}, \quad \alpha\in[-1,1].$

Applications with Stochastic Matrices

An important application of fractional matrix powers is in discrete-time Markov chains, which arise in areas including finance and medicine. A transition matrix for a Markov process is a matrix whose $(i,j)$ element is the probability of moving from state $i$ to state $j$ over a time step. It has nonnegative entries and the rows sum to $1$ , so it is a stochastic matrix. In practice, a transition matrix may be estimated for a certain time period, say one year, but a transition matrix for a shorter period, say one month, may be needed. If $A$ is a transition matrix for a time period $p$ then a stochastic $p$ th root of $A$ is a transition matrix for a time period a factor $p$ smaller. Therefore $p = 12$ (years to months) and $p = 7$ (weeks to days) are among the values of interest. Unfortunately, $A^{1/p}$ is not necessarily a stochastic matrix. Moreover, $A$ can have a stochastic $p$ th root that is not $A^{1/p}$ . For example, the stochastic matrix

$\notag A = \left[\begin{array}{ccc} 0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0\\ \end{array} \right]$

has principal square root

$\notag A^{1/2} = \frac{1}{3} \left[\begin{array}{rrr} 2 & 2 & -1 \\ -1 & 2 & 2 \\ 2 & -1 & 2 \end{array} \right],$

but $A^{1/2}$ is not stochastic because of the negative elements. The square root

$\notag Y = \left[\begin{array}{ccc} 0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0\\ \end{array} \right]$

is stochastic, though. (Interestingly, $A$ is also a square root of $Y$ !)

A wide variety configurations is possible as regards existence, nature (primary or nonprimary), and number of stochastic roots. Higham and Lin (2011) delineate the various possibilities that can arise. They note that the stochastic lower triangular matrix

$\notag A_n = \begin{bmatrix} 1 & & & \\ \frac{1}{2} & \frac{1}{2} & & \\ \vdots & \vdots &\ddots & \\ \frac{1}{n} & \frac{1}{n} &\cdots & \frac{1}{n} \end{bmatrix}$

has a stochastic $p$ th root, namely $A_n^{1/p}$ , for all $p$ . For example, to three significant figures,

$\notag A_6^{1/3} = \begin{bmatrix} 1.000 & & & & & \\ 0.206 & 0.794 & & & & \\ 0.106 & 0.201 & 0.693 & & & \\ 0.069 & 0.111 & 0.190 & 0.630 & & \\ 0.050 & 0.075 & 0.109 & 0.181 & 0.585 & \\ 0.039 & 0.056 & 0.076 & 0.107 & 0.172 & 0.550 \\ \end{bmatrix}.$

The existence of stochastic roots of stochastic matrices is connected with the embeddability problem, which asks when a nonsingular stochastic matrix $A$ can be written $A = \mathrm{e}^Q$ for some $Q$ with $q_{ij} \ge 0$ for $i\ne j$ and $\sum_{j=1}^n q_{ij} = 0$ , $i=1\colon n$ . Kingman showed in 1962 that this condition holds if and only if for every positive integer $p$ there exists a stochastic $X_p$ such that $A = X_p^p$ .

Applications in Fractional Differential Equations

Fractional matrix powers arise in the numerical solution of differential equations of fractional order, especially partial differential equations involving fractional Laplace operators. Here, the problem may be one of computing $A^\alpha b$ , in which case for large problems it is preferable to directly approximate $A^\alpha b$ , for example by Krylov methods or quadrature methods, rather than to explicitly compute $A^\alpha$ .

References

This is a minimal set of references, which contain further useful references within.

Brian Davies, Embeddable Markov Matrices, Electronic J. Probability 15, 1474–1486, 2010.
Roberto Garrappa and Marina Popolizio, On the Use of Matrix Functions for Fractional Partial Differential Equations, Math. Comput. Simulation C-25(81), 1045–1056, 2011.
Nicholas J. Higham, Functions of Matrices: Theory and Computation, Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, 2008.
Nicholas J. Higham and Lijing Lin, On $p$ th Roots of Stochastic Matrices, Linear Algebra Appl. 435(3), 448–463, 2011.
Nicholas Higham and Lijing Lin, An Improved Schur–Padé Algorithm for Fractional Powers of a Matrix and their Fréchet Derivatives, SIAM J. Matrix Anal. Appl. 34(3), 1341–1360, 2013.
Emmanuel Lorin and Simon Tian, A Numerical Study of Fractional Linear Algebraic Systems, Math. Comput. Simulation 182, 495–513, 2021.

What Is the Matrix Unwinding Function?

Care is needed when dealing with multivalued functions because identities that hold for positive scalars can fail in the complex plane. For example, it is not always true that $(z-1)^{1/2}(z+1)^{1/2} = (z^2-1)^{1/2}$ or $\log(z_1 z_2) = \log z_1 + \log z_2$ for all $z,z_1,z_2\in\mathbb{C}$ . Here, the square root is the principal square root (the one lying in the right half-plane) and the logarithm is the principal logarithm (the one with imaginary part in $(-\pi,\pi]$ ).

A powerful tool for dealing with multivalued complex functions is the unwinding number, defined for $z\in\mathbb{C}$ by

$\notag \mathcal{U}(z) = \displaystyle\frac{z - \log \mathrm{e}^z}{2\pi \mathrm{i}}.$

The unwinding number provides a correction term for the putative identity $\log \mathrm{e}^z = z$ , in that

$\notag \qquad\qquad\qquad\qquad z = \log \mathrm{e}^z + 2\pi \mathrm{i}\, \mathcal{U}(z) \qquad\qquad\qquad\qquad (*)$

for all $z$ .

A useful formula for the unwinding number is

$\notag \mathcal{U}(z) = \left\lceil\displaystyle\frac{\mathrm{Im} z - \pi}{2\pi}\right\rceil,$

where $\lceil\cdot\rceil$ is the ceiling function, which returns the smallest integer greater than or equal to its argument. It follows that $\mathcal{U}(z) = 0$ if and only if $\mathrm{Im} z \in (-\pi, \pi]$ . Hence $\log \mathrm{e}^z = z$ if and only if $\mathrm{Im} z \in (-\pi, \pi]$ .

The unwinding number provides correction terms for various identities. For example, for $z_1,z_2\in\mathbb{C}$ , replacing $z$ by $\log z_1 \pm \log z_2$ in $(*$ ), we have

$\notag \begin{aligned} \log z_1 \pm \log z_2 &= \log \bigl( \mathrm{e}^{\log z_1 \pm \log z_2} \bigr) + 2\pi\mathrm{i} \, \mathcal(\log z_1 \pm \log z_2)\\ &= \log \bigl(\mathrm{e}^{\log z_1} \mathrm{e}^{\pm \log z_2} \bigr) + 2\pi\mathrm{i} \, \mathcal(\log z_1 \pm \log z_2)\\ &= \log \bigl( z_1 z_2^{\pm 1} \bigr) + 2\pi\mathrm{i} \, \mathcal(\log z_1 \pm \log z_2). \end{aligned}$

This gives the identities

$\notag \begin{aligned} \log (z_1 z_2) &= \log z_1 + \log z_2 - 2\pi \mathrm{i}\, \mathcal{U}(\log z_1 +\log z_2), \\ \qquad\qquad\qquad \log (z_1/z_2) &= \log z_1 - \log z_2 - 2\pi \mathrm{i}\,\mathcal{U}(\log z_1 - \log z_2). \qquad\qquad\qquad (\#) \end{aligned}$

Note that in textbooks one can find identities such as $\log (z_1 z_2) = \log z_1 + \log z_2$ , in which each occurrence of $\log$ is interpreted as a possibly different branch. For computational purposes we want formulas that contain a specific branch, usually the principal branch.

An application of the unwinding number to matrix functions is in computing the logarithm of a $2\times 2$ upper triangular matrix. For any function $f$ , we have

$\notag f\left( \begin{bmatrix} \lambda_1 & t_{12} \\ 0 & \lambda_2 \end{bmatrix} \right) = \begin{bmatrix} f(\lambda_1) & t_{12} f[\lambda_1,\lambda_2] \\ 0 & f(\lambda_2) \end{bmatrix},$

where the divided difference

$\notag f[\lambda_1,\lambda_2] = \begin{cases} \displaystyle\frac{f(\lambda_2)-f(\lambda_1)}{\lambda_2-\lambda_1}, & \lambda_1 \ne \lambda_2, \\ f'(\lambda_1), & \lambda_1 = \lambda_2. \end{cases}$

When $\lambda_1 \approx \lambda_2$ this formula suffers from numerical cancellation. For the logarithm, we can rewrite it, using $(\#)$ , as

$\notag \begin{aligned} \log\lambda_2 - \log\lambda_1 &= \log \left(\frac{\lambda_2}{\lambda_1}\right) + 2\pi \mathrm{i} \, \mathcal{U}(\log \lambda_2 - \log \lambda_1) \\ &= \log \left(\frac{1+z}{1-z}\right) + 2\pi \mathrm{i}\, \mathcal{U}(\log \lambda_2 - \log \lambda_1), \end{aligned}$

where $z = (\lambda_2-\lambda_1)/(\lambda_2+\lambda_1)$ . Using the hyperbolic arc tangent, defined by

$\notag \mathrm{atanh}(z) = \frac{1}{2}\log\left( \displaystyle\frac{1+z}{1-z} \right),$

we obtain

$\notag f[\lambda_1,\lambda_2] = \displaystyle\frac{2\mathrm{atanh}(z) + 2\pi \mathrm{i}\, \mathcal{U}(\log \lambda_2 - \log \lambda_1)}{\lambda_2-\lambda_1}, \quad \lambda_1 \ne \lambda_2.$

Assuming that we have an accurate $\mathrm{atanh}$ function this formula will provide an accurate value of $f[\lambda_1,\lambda_2]$ provided that $z$ is not too close to $\pm 1$ (the singularities of $\mathrm{atanh}$ ) and not too large. This formula is used in the MATLAB function logm.

Matrix Unwinding Function

The unwinding number leads to the matrix unwinding function, defined for $A\in\mathbb{C}^{n\times n}$ by

$\notag \mathcal{U}(A) = \displaystyle\frac{A - \log \mathrm{e}^A}{2\pi \mathrm{i}}.$

Here, $\log$ is the principal matrix logarithm, defined by the property that its eigenvalues have imaginary parts in the interval $(-\pi,\pi]$ . It can be shown that $\mathcal{U}(A) = 0$ if and only if the imaginary parts of all the eigenvalues of $A$ lie in the interval $(-\pi, \pi]$ . Furthermore, $\mathcal{U}(A)$ is a diagonalizable matrix with integer eigenvalues.

As an example, the matrix

$\notag A = \left[\begin{array}{rrrr} 3 & 1 & -1 & -9\\ -1 & 3 & 9 & -1\\ -1 & -9 & 3 & 1\\ 9 & -1 & -1 & 3 \end{array}\right], \quad \Lambda(A) = \{ 2\pm 8\mathrm{i}, 4 \pm 10\mathrm{i} \}$

has unwinding matrix function

$\notag X = \mathcal{U}(A) = \mathrm{i} \left[\begin{array}{rrrr} 0 & -\frac{1}{2} & 0 & \frac{3}{2}\\ \frac{1}{2} & 0 & -\frac{3}{2} & 0\\ 0 & \frac{3}{2} & 0 & -\frac{1}{2}\\ -\frac{3}{2} & 0 & \frac{1}{2} & 0 \end{array}\right], \quad \Lambda(X) = \{ \pm 1, \pm 2 \}.$

In general, if $A$ is real then $\mathcal{U}(A)$ is pure imaginary as long as $A$ has no eigenvalue with imaginary part that is an odd multiple of $\pi$ .

The matrix unwinding function is useful for providing correction terms for matrix identities involving multivalued functions. Here are four useful matrix identities, along with cases in which the correction term vanishes. See Aprahamian and Higham (2014) for proofs.

For nonsingular $A$ and $\alpha,\beta\in\mathbb{C}$ ,
$\notag (A^\alpha)^{\beta} = A^{\alpha\beta} \mathrm{e}^{-2\beta\pi \mathrm{i}\, \mathcal{U}(\alpha\log A)}.$

If $\beta$ is an integer then the correction term is $I$ . If $\alpha\in(-1,1]$ and $\beta = 1/\alpha$ then $\mathcal{U}(\alpha\log A) = 0$ and so

$\notag (A^\alpha)^{1/\alpha} = A, \quad \alpha \in [-1,1],$

and this equation is obviously true for $\alpha = -1$ , too.
If $A$ and $B$ are nonsingular and $AB = BA$ then
$\notag \log(AB^{\pm1}) = \log A \pm \log B - 2\pi \mathrm{i}\, \mathcal{U}(\log A \pm \log B).$

If $\arg\lambda_i + \arg\mu_i \in(-\pi,\pi]$ for every eigenvalue $\lambda_i$ of $A$ and the corresponding eigenvalue $\mu_i$ of $B$ (there is a correspondence because of the commutativity of $A$ and $B$ , which implies that they are simultaneously unitarily diagonalizable), then $\log(AB^{\pm 1}) = \log A \pm \log B$ .
If $A$ and $B$ are nonsingular and $AB = BA$ then for any $\alpha\in\mathbb{C}$ ,
$\notag (AB)^\alpha = A^\alpha B^\alpha \mathrm{e}^{-2\pi\, \alpha \mathrm{i}\, \mathcal{U}(\log A + \log B)}.$

If $\alpha$ is an integer or the eigenvalues of $A$ and $B$ have arguments in $(-\pi/2,\pi/2]$ then $(AB)^\alpha = A^\alpha B^\alpha$ .
For nonsingular $A$ and $\alpha\in\mathbb{C}$ .
$\notag \log A^{\alpha} = \alpha \log A - 2\pi \mathrm{i}\, \mathcal{U}(\alpha \log A).$

If $\alpha\in(-1,1]$ then $\log A^{\alpha} = \alpha \log A$ , and this equation also holds for $\alpha = -1$ if $A$ has no negative eigenvalues.

The matrix unwinding function can be computed by an adaptation of the Schur–Parlett algorithm. The algorithm computes a Schur decomposition and re-orders it into a block form with eigenvalues having the same unwinding number in the same diagonal block. The unwinding function of each diagonal block is then a multiple of the identity and the off-diagonal blocks are obtained by the block Parlett recurrence. This approach gives more accurate results than directly evaluating $\mathcal{U}(A)$ from its definition in terms of the matrix logarithm and natrix exponential. A MATLAB code unwindm is available at https://github.com/higham/unwinding

Matrix Argument Reduction

The matrix unwinding function can be of use computationally for reducing the size of the imaginary parts of the eigenvalues of a matrix. The function

$\notag \mathrm{mod}(A) = A - 2\pi\mathrm{i}\, \mathcal{U}(A)$

has eigenvalues $\lambda$ with $\mathrm{Im} \lambda \in(-\pi,\pi]$ . Using $\mathrm{mod}(A)$ in place of $A$ can be useful in computing the matrix exponential by the scaling and squaring algorithm because $\mathrm{e}^A = \mathrm{e}^{\mathrm{mod}(A)}$ and $\mathrm{mod}(A)$ can have a much smaller norm than $A$ , giving potential reductions in cost. Combined with the Schur decomposition-based algorithm for $\mathcal{U}(A)$ mentioned above, this idea leads to a numerical method for $\mathrm{e}^A$ . See Aprahamian and Higham (2014) for details.

Round Trip Relations

If you apply a matrix function and then its inverse do you get back to where you started, that is, is $f^{-1}(f(z)) = z$ ? In principle yes, but if the inverse is multivalued the answer is not immediate. The matrix unwinding function is useful for analyzing such round trip relations. As an example, if $A$ has no eigenvalues with real part of the form $k \pi$ for an integer $k$ , then

$\notag \mathrm{acos}(\cos A) = \bigl(A-2\pi\,\mathcal{U} (\mathrm{i} A)\bigr)\mathrm{sign} \bigl(A-2\pi\mathcal{U}( \mathrm{i} A)\bigr).$

Here, $\mathrm{acos}$ is the principal arc cosine defined in Aprahamian and Higham (2016), where this result and analogous results for the arc sine, arc hyperbolic cosine, and arc hyperbolic sine are derived; and $\mathrm{sign}$ is the matrix sign function.

History

The unwinding number was introduced by Corless, Hare and Jeffrey in 1996, to help implement computer algebra over the complex numbers. It was generalized to the matrix case by Aprahamian and Higham (2014).

References

This is a minimal set of references, which contain further useful references within.

Mary Aprahamian and Nicholas J. Higham, The Matrix Unwinding Function, with an Application to Computing the Matrix Exponential, SIAM J. Matrix Anal. Appl. 35(1), 88–109, 2014.
Mary Aprahamian and Nicholas J. Higham, Matrix Inverse Trigonometric and Inverse Hyperbolic Functions: Theory and Algorithms, SIAM J. Matrix Anal. Appl. 37(4), 1453–1477, 2016.
Robert Corless and David Jeffrey, The Unwinding Number, SIGSAM Bull 30(2), 28–35, 1996.
David Jeffrey, D. E. G. Hare and Robert Corless, Unwinding the Branches of the Lambert W Function, Math. Scientist 21, 1–7, 1996.
Nicholas J. Higham, Functions of Matrices: Theory and Computation, Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, 2008.

Month: December 2020

Top Ten Posts of 2020

What Is a Modified Cholesky Factorization?

Example

References

Related Blog Posts

What Is the Matrix Sign Function?

Application to Sylvester Equation

Application to the Eigenvalue Problem

Computing the Matrix Sign Function

Relation to Matrix Square Root and Polar Decomposition

References

Related Blog Posts

What Is a Fractional Matrix Power?

Computation

Inverse Function

Backward Error

Applications with Stochastic Matrices

Applications in Fractional Differential Equations

References

Related Blog Posts

What Is the Matrix Unwinding Function?

Matrix Unwinding Function

Matrix Argument Reduction

Round Trip Relations

History

References

Related Blog Posts

Share this:

Example

References

Related Blog Posts

Share this:

Application to Sylvester Equation

Application to the Eigenvalue Problem

Computing the Matrix Sign Function

Relation to Matrix Square Root and Polar Decomposition

References

Related Blog Posts

Share this:

Computation

Inverse Function

Backward Error

Applications with Stochastic Matrices

Applications in Fractional Differential Equations

References

Related Blog Posts

Share this:

Matrix Unwinding Function

Matrix Argument Reduction

Round Trip Relations

History

References

Related Blog Posts

Share this: